こんにちは。2020年1月より１か月間、AI Lab Econチームでインターンをしていました浅川です。本稿では、今回のインターンシップ中に取り組んだ「UpLift Modeling を使った最適クリエイティブ数予測モデルの開発」についてご紹介します。

1. 問題設定
天気予報、音楽再生、乗り換え検索。スマートフォンをお使いの方なら、恐らく毎日のように多種多様なアプリを使っていると思います。皆さんの中にはアプリに表示される広告をクリックして、実際に購入したり、店舗に足を運んだりした経験のある方も少なくないと思います。
このアプリ内広告。ご存知の方も多いと思いますが、ほとんどがスマートフォンのアプリを開くと同時に、リアルタイムのオークション(Real Time Bidding, RTB)によって入札され、どの広告主が広告配信できるかが決まります。その後、オークションに勝った広告主は、その配信枠に対して次にどの広告を配信するかを決定します。
通常、ある広告枠に対して、ある広告主から受注した広告の種類は複数あることが一般的です。例えば、ある広告主がセール広告を配信する場合、セール期間中の目玉商品が複数あり、その結果、広告（以下ではクリエイティブと言います）の種類も複数用意されています。
そのため、DSPといわれる広告配信システムはオークションに勝った広告枠に対して、複数あるクリエイティブから最適なものを選ばなければいけません。それだけでなく、あるユーザーに対して、広告主の広告を複数回配信する場合、どのクリエイティブを選択すべきなのかという問題も生じます。例えば、同じユーザーに対して、同じクリエイティブを繰り返して配信すべきなのか、もしくは、異なるクリエイティブを１度ずつ配信すべきなのか、についてはあまり自明ではありません。
このような背景から、今回のインターンでは主に以下のような問題に取り組みました。

・クリエイティブの種類によって広告効果は変わるのか？
・それぞれのユーザーにとって最適なクリエイティブの種類はいくらなのか？
・仮に最適なクリエイティブ数がユーザーによって違う場合、その違いを生み出している特徴量は何なのか？

2. 検証方法
2.1. アップリフトモデリングとは
今回使用したのは、広告効果の予測に広く使われているアップリフトモデリングという手法です（詳細なサーベイはGutierrez and Gerardy 2017を参照のこと）。アップリフトモデリングではまず、データを訓練データとテストデータに分けたのち、訓練データのアウトカム変数 \(Y_i\), 処置変数 \(W_i\), そして特徴量 \(X_i\) を用いて学習器を作成します。ただし、以下表１のように、広告を実際に見た人（\(W_i=1\)）が「見ていなかった（\(W_i=0\)）」時のアウトカムや、広告を実際は見なかった人（\(W_i=0\)）が「見た（\(W_i=1\)）」時のアウトカムについては欠損データとして、観察することはできません（因果推論の根本問題）。

表１

そのため、通常はA/Bテストによって、特徴量に由来するバイアスを取り除きます。これによって、特徴量が類似するグループについては \(E[Y_i (1)| W_i=1, X_i] と E[Y_i (0)| W_i=1, X_i]\) の差分を取ることで、グループ\(X_i\) における因果効果を推定することができます。
ここから、因果推論から予測の話に移ります。次に、この学習器を使ってテストデータの\(X_i\) から処置を受けた場合（\(W_i=1\)）と受けなかった場合（\(W_i=0\)）についてそれぞれ\(Y_i\) の予測値 \(E[Y_i | W_i=1, X_i],E[Y_i | W_i=0, X_i]\)を計算します。ここで得られた\(Y_i\) の予測値について各個人ごとに差分を取ると、以下のように個人レベルの因果効果の予測値\(E[τ_i (X_i )]\)を計算することができます。

$$E[τ_i (X_i )]=E[Y_i | W_i=1, X_i]-E[Y_i | W_i=0, X_i]$$

　これによって予測された個人レベルの因果効果\((τ_i)\)が高い順にユーザーを並べて、より処置効果が高いユーザーのみに処置を当てようというのがアップリフトモデリングの基本的なアイデアになります。

2.2. アップリフトモデリングの利点
アップリフトモデリングを使うことで、特徴量\(X_i\) の情報のみから個人レベルの因果効果\((τ_i)\)を予測することができます。そのため、アップリフトモデリングには以下のような利点があると考えられます。

①何割くらいの人に広告を配信することが最も費用対効果が高いかを推論することができます。
②\(E[τ(X)]\) を用いてユーザーをグループ分けすることで、どのような特徴を持つグループで広告効果が最大になったのかを検討することができます。(c.f. Kawanaka and Moriwaki 2019)
③広告の種類が複数ある状況で、何種類の広告を当てることが広告効果を最大化するのかを検討することができます。（今回のインターンでの取り組み）

2.3. アップリフトモデリングの評価指標
それでは、アップリフトモデリングがうまく個人レベルの因果効果を予測できているかどうかは、どのように評価すればいいのでしょうか。これについて、既存研究ではAUUC (Areas Under the Uplift Curves)を用いて評価することが一般的です（詳細はRzepakowski and Jaroszewicz 2012を参照のこと）。以下では、簡単にAUUCの計算方法を紹介します。

①訓練データ\({Y_i, W_i, X_i}\)を使って\(τ_i\) を予測する学習器を作成し、テストデータの\(X_iから\widehat{\tau_i}\left(X_i\right)\)を予測します。
②\(\widehat{\tau_i}\left(X_i\right)\) が大きい順にサンプルを並べます。
③テストデータの\({Y_i, W_i }\)を使って個人 \(i\) までのCVR（コンバージョン率）を処置群、統制群それぞれについて計算し、差分を個人 \(i\) の時点でのアップリフト (\(Lift_i\))とします。
④ランダムにサンプルを並べた時の個人 \(i\) の時点での CVRを\(Baseline_i\)とします。
⑤最後にアップリフトカーブ (\(Lift_i\))とベースラインカーブ (\(Baseline_i\))の差分をとり、その総和をAUUCとします。

うまく個人レベルの因果効果が予測できている場合、アップリフトカーブの形状は以下のようになります。具体的に、原点から順に累積の因果効果が高くなり、ピークの点を境に累積の因果効果が低下していくような形状となることが理想とされます。以下図１の例の場合は、全体のうち約25%で累積の因果効果が最も高くなるため、全体のうち約25%のユーザーに広告を当てればいいと結論づけることができます。

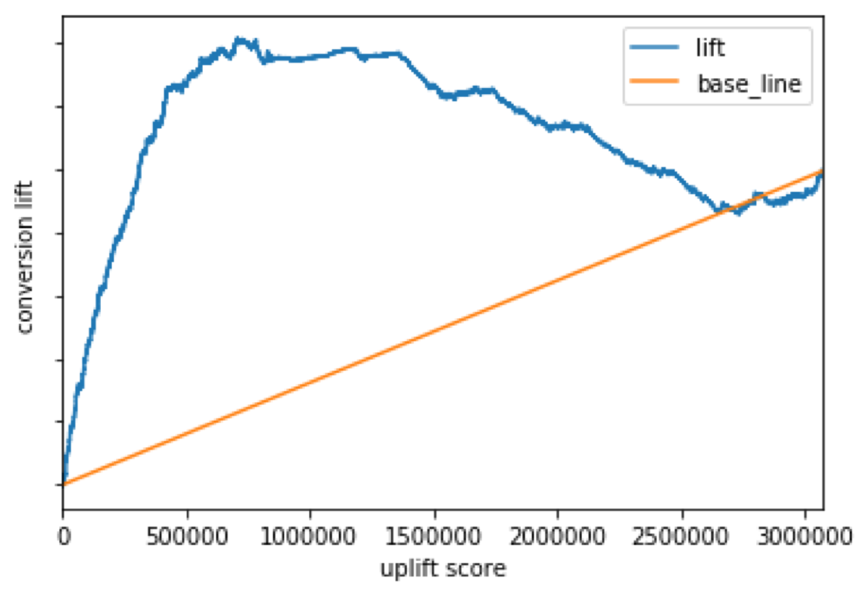
　図１

3. 観察データにおけるアップリフトモデリング
3.1. 観察データを用いる場合の問題点
2.1で述べたように、通常、アップリフトモデリングはA/Bテストを用いたRCTを前提としています。しかしながら、広告データの分析では、仮に広告を配信するグループ（処置群）か否かをランダムに分類した場合でも、広告が配信されるかどうかは広告の配信期間中に対象となるアプリを使用した頻度や競合他社とのオークションの勝敗によって決まるため、配信グループに必ずしも広告が配信されるかどうか（実際に処置を受けたかどうか）は定かではありません。そのため、個人レベルの因果効果を推定するためには、処置群の中でその個人が実際にどれくらい処置を受けやすいかを補正する必要があります。

3.2. 傾向スコアを用いた補正方法
先行研究（Athey and Imbens 2015, Gutierrez and Gerardy 2017など参照のこと）でも提唱されているように、トリートメントが１種類の場合は傾向スコア \(p ̂(X_i)\) で処置の有無を逆重み付けすることで、処置の受けやすさを補正した上で個人レベルの因果効果\(\widehat{\tau_i}\left(X_i\right)\) を予測することができます。

$$Y_i^*=Y_i (1)\frac{ W_i}{p ̂(X_i)}+Y_i (0)\frac{1-W_i}{1-p ̂(X_i)}$$

$$E[Y_i^* |X_i]=τ ̂(X_i)$$

この場合、\(E[Y_i^* |X_i]\) を予め学習しておくことで未知の\(X_i\) についても\(\widehat{\tau_i}\left(X_i\right)\) の予測ができます。

3.3. トリートメントが複数ある場合の傾向スコアを用いた補正方法
今回のように、クリエイティブの種類が複数ある、つまりトリートメントが複数ある場合、3.2のような手法をそのまま使うことはできません。なぜなら、処置を受けるか受けないかに加えて、全体の中である処置\( T\) を受ける確率で処置の有無を逆重み付けする必要があるからです。本研究では、Imbens (2000) やFeng et al (2012)などで提案されている一般化傾向スコア(GPS)を用いて逆重み付けすることを試みました。これによって、ある処置の受けやすさを補正した上で個人レベルの因果効果\(τ^{GPS} (X_i)\)を予測できるようになります。

$$Y_i^{GPS} (t)=Y_i (1) \frac{W_i ∑_{T=0}^Mr(T,X_i)}{r(T=t,X_i)}+Y_i (0) \frac{(1-W_i)∑_{T=0}^Mr(T,X_i)}{r(0,X_i)}$$

$$E[Y_i^{GPS} |X_i]=τ^{GPS} (X_i)$$

$$Where ∑_{T=0}^Mr(T,X_i)=1$$

なお、今回は傾向スコアの推定に、広く使われているロジスティック回帰を使用しました。その上で、個人レベルの因果効果を予測する際には、最小２乗推定を使用しました。

４. 使用データの構成と特徴

・今回使用したのは、実際の広告データです。
・配信期間最終日の時点で実際に店舗に行っていたら１をとるダミー変数を、今回はアウトカムとして利用します。

実際にそれぞれのユーザーは何種類のクリエイティブを見ていたのでしょうか？以下に示すのは、実際に見たクリエイティブ数について描いたヒストグラムを描いたものです。これによると、ほどんどのユーザーが１種類しかクリエイティブを見なかったことがわかります。次の節では、広告効果を最も高くするために、各ユーザーにとって実際は何種類のクリエイティブを見ることが良かったのかについて議論を行います。

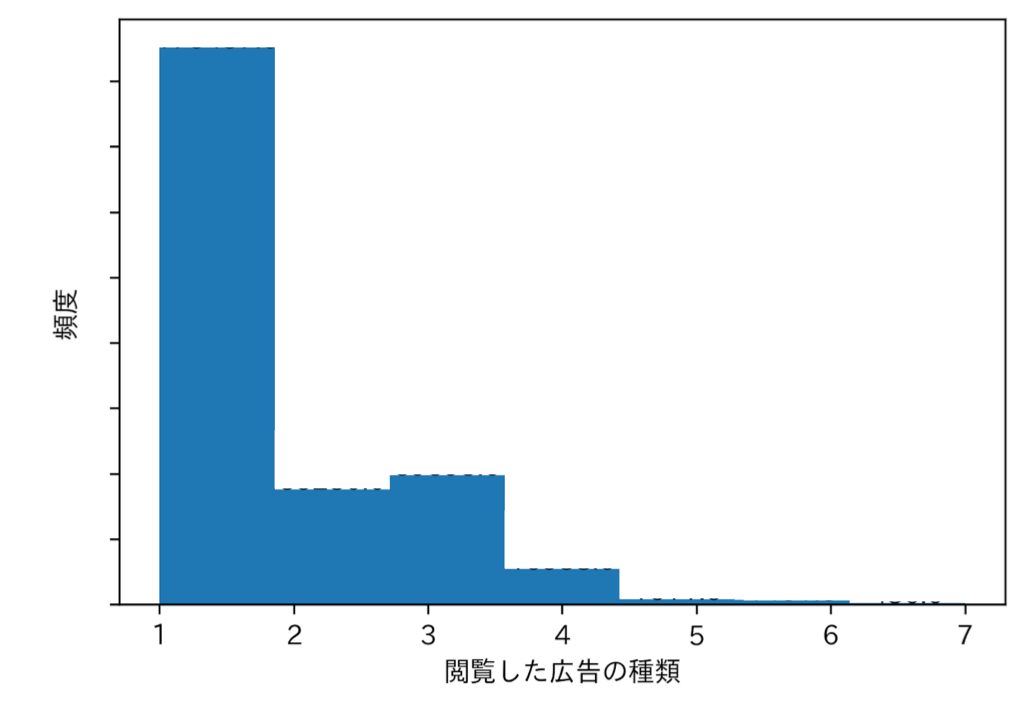
図２

5. 結果
まず、AUUCの数値からアップリフトカーブがうまくかけているかを検証していきます。
① クリエイティブが１種類の場合

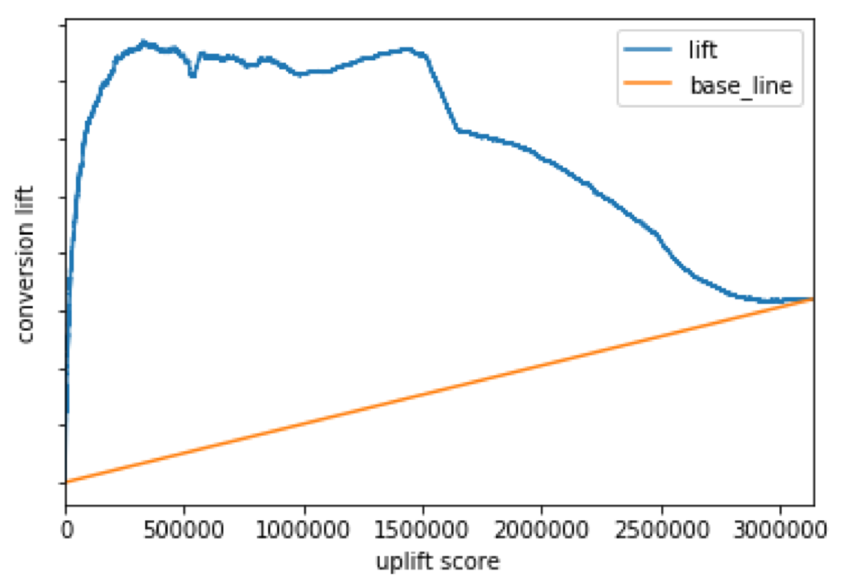
図３

アップリフトカーブはうまくかけていると考えられます。広告効果が最も高くなった位置（累積相対度数）はアップリフトスコア上位約10%でした。

② クリエイティブが２種類の場合

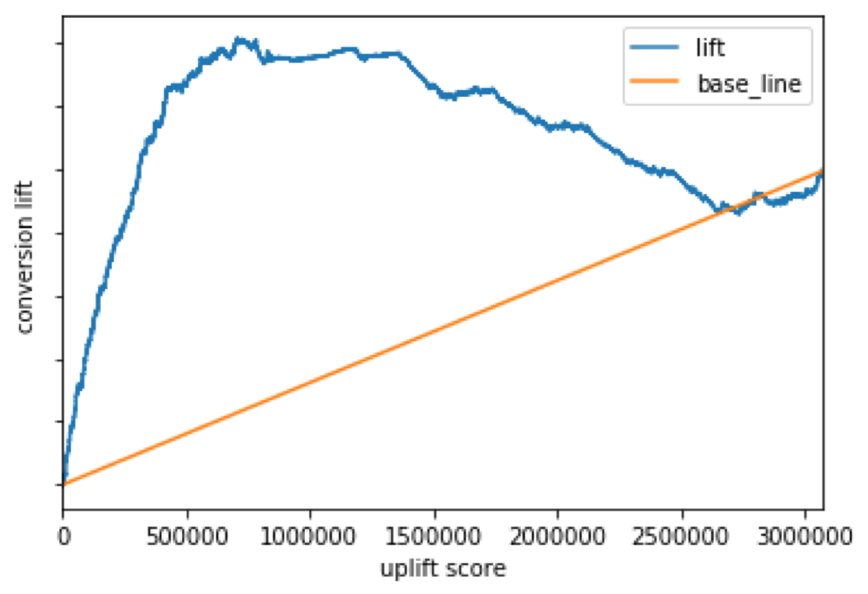
図４

このケースもアップリフトカーブもうまくかけていると考えられます。広告効果が最も高くなった累積相対度数はアップリフトスコア上位約22.5%でした。

③ クリエイティブが3種類の場合

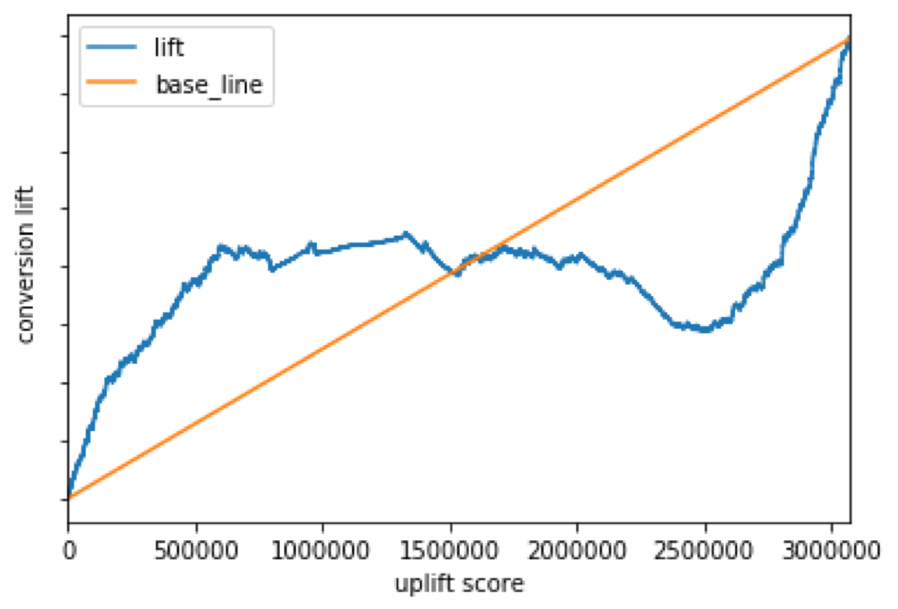
図５

AUUCはマイナスで、アップリフトカーブは1,500,000人を境にベースラインを下回っています。ここから、クリエイティブが３種類の場合は広告の効果が逆に効いてしまう状況がみてとれます。なお、広告効果が最も高くなった累積相対度数はアップリフトスコア上位約20%でした。

④ クリエイティブが４〜７種類の場合
クリエイティブ数が４〜７種類については、すべて同様の形状でありかつ、アップリフトカーブもうまくかけていたため、図示は省略します。

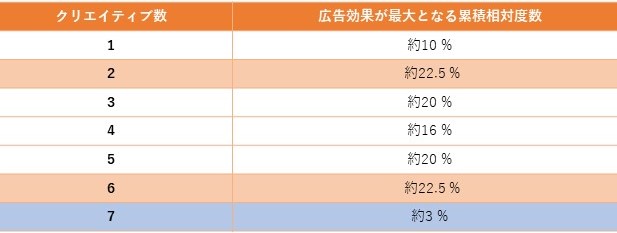
以上の結果をまとめたものが以下の表になります。なお、累積相対度数が最も高くなったのはクリエイティブ数が２と６のケース。累積相対度数が最少となったのはクリエイティブ数が７のケースでした。

表２

 

最後に、①〜④より作成した予測モデルを使って、各個人についてクリエイティブ数が０〜７だった場合の反実仮想的な広告効果をそれぞれ予測しました。そのうち、各個人の中で最も広告効果(アップリフト)が高かったものを最適クリエイティブ数として、以下にヒストグラムを描きました。

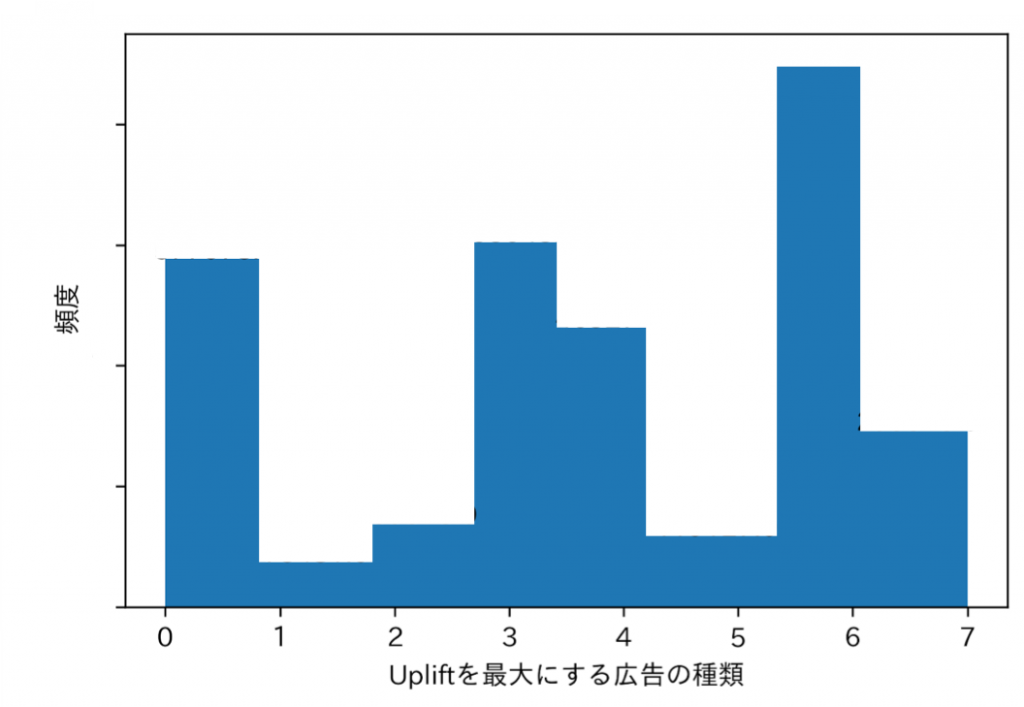
図６

　実際に閲覧されたクリエイティブ数のヒストグラム（図２）と比較すると、特にクリエイティブ数が６種類のところで、頻度が大幅に増加しています。このことから、最適クリエイティブ数は６にも関わらず、ほとんどのユーザーはそこまで多くの種類のクリエイティブ数を閲覧できていないことが分かりました。

6. 最後に
今回のインターンシップはAI Lab Econチームの森脇さんからの紹介で実現しました。
序盤は機械学習やPythonなど、基本的な知識の習得に必死でしたが、実装や理論で分からない部分は気軽にラボの皆さんに相談できたので、スムーズに研究に取り組むことができました。メンターの森脇さんには、毎日最低30分のMTGの時間を割いていただき、研究テーマに関するディスカッションに加えて、研究生活を送る上で重要な様々なことを教えていただきました。また、社内には経済学をバックグラウンドとする社員も複数人いて、ディスカッションを通じて、非常に多くの刺激を受けることができました。
最後になりますが、これまで、就活はおろかインターンシップさえ経験したことが無かった私に文字通り０から、成長する機会を与えてくださったラボメンバーの皆さんには感謝の気持ちでいっぱいです。１ヶ月間という短い期間でしたが、本当にお世話になりました。ありがとうございました。

参考文献
Athey, S., & Imbens, G. W. (2015). Machine learning methods for estimating heterogeneous causal effects. stat, 1050(5), 1-26.

Feng, P., Zhou, X. H., Zou, Q. M., Fan, M. Y., & Li, X. S. (2012). Generalized propensity score for estimating the average treatment effect of multiple treatments. Statistics in medicine, 31(7), 681-697.

Gutierrez, P., & Gérardy, J. Y. (2017, July). Causal inference and uplift modelling: A review of the literature. In International Conference on Predictive Applications and APIs (pp. 1-13).

Imbens, G. W. (2000). The role of the propensity score in estimating dose-response functions. Biometrika, 87(3), 706-710.

Kawanaka, S., & Moriwaki, D. (2019, November). Uplift modeling for location-based online advertising. In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on Location-based Recommendations, Geosocial Networks and Geoadvertising (pp. 1-4).

Rzepakowski, P., & Jaroszewicz, S. (2012). Decision trees for uplift modeling with single and multiple treatments. Knowledge and Information Systems, 32(2), 303-327.