\(\newcommand{\bm}[1]{\boldsymbol{#1}}\newcommand\bmu{\bm{\mu}}\newcommand{\argmax}{\text{argmax}}\newcommand{\PP}{\mathbb{P}}\newcommand{\EE}{\mathbb{E}} \)AI Lab 強化学習チームの蟻生開人です。本記事では、二腕固定予算最適腕識別(A/Bテスト)における最適な手法について考察を行った論文を紹介します。昨年夏のAI Lab リサーチインターンシップでスウェーデン王立工科大学(KTH)博士課程のPo-An Wangさんが取り組んだもので、その成果がICML 2024に採択されました。

On Universally Optimal Algorithms for A/B Testing
Po-An Wang, Kaito Ariu, Alexandre Proutiere
International Conference on Machine Learning (ICML) 2024

はじめに

A/Bテストは、Webマーケティングなどで一般的に用いられる手法で、ユーザーの反応に基づいて最適な施策を見つけ出すために利用されます。具体例として、ウェブサイトのUI最適化を考えます。ここでは2つのUI候補AとBがあり、どちらのUIがより効果的かを検証したいとします。ユーザーから得ることのできる反応の総数を\(T\)回とします。

通常のA/Bテストでは、UI候補AとUI候補Bに対してそれぞれ50%ずつ、つまり\(T/2\)回ずつ固定割合で割り当てて反応を集めます。そして、肯定的な反応がより多く得られたUI候補を良いUIとして採用する形式が一般的です。一方で、このA/Bテストを逐次的意思決定問題として捉え、テスト中に得られたユーザー反応に基づいて各施策への割り当てを適応的に変える方法もあります。

しかし、これまでの研究では、このような適応的な割り当てが実際にどの程度効果的であるかは明らかにされていませんでした。本研究では、特定の状況下で施策の適応的な割り当てが結果を改善しないことを理論的および実験的に明らかにしました。

問題設定

本論文の問題設定を述べます。ベルヌーイ報酬下の二腕固定予算最適腕識別問題を考察します。この問題では、アルゴリズムは各時刻ごとにサンプルする腕を一本選び、選んだ腕に対応する報酬を観測することを\(T\)回繰り返します。\(T\)回の観測の後、アルゴリズムは期待値が最も高い腕(最適腕)を推定して出力します。

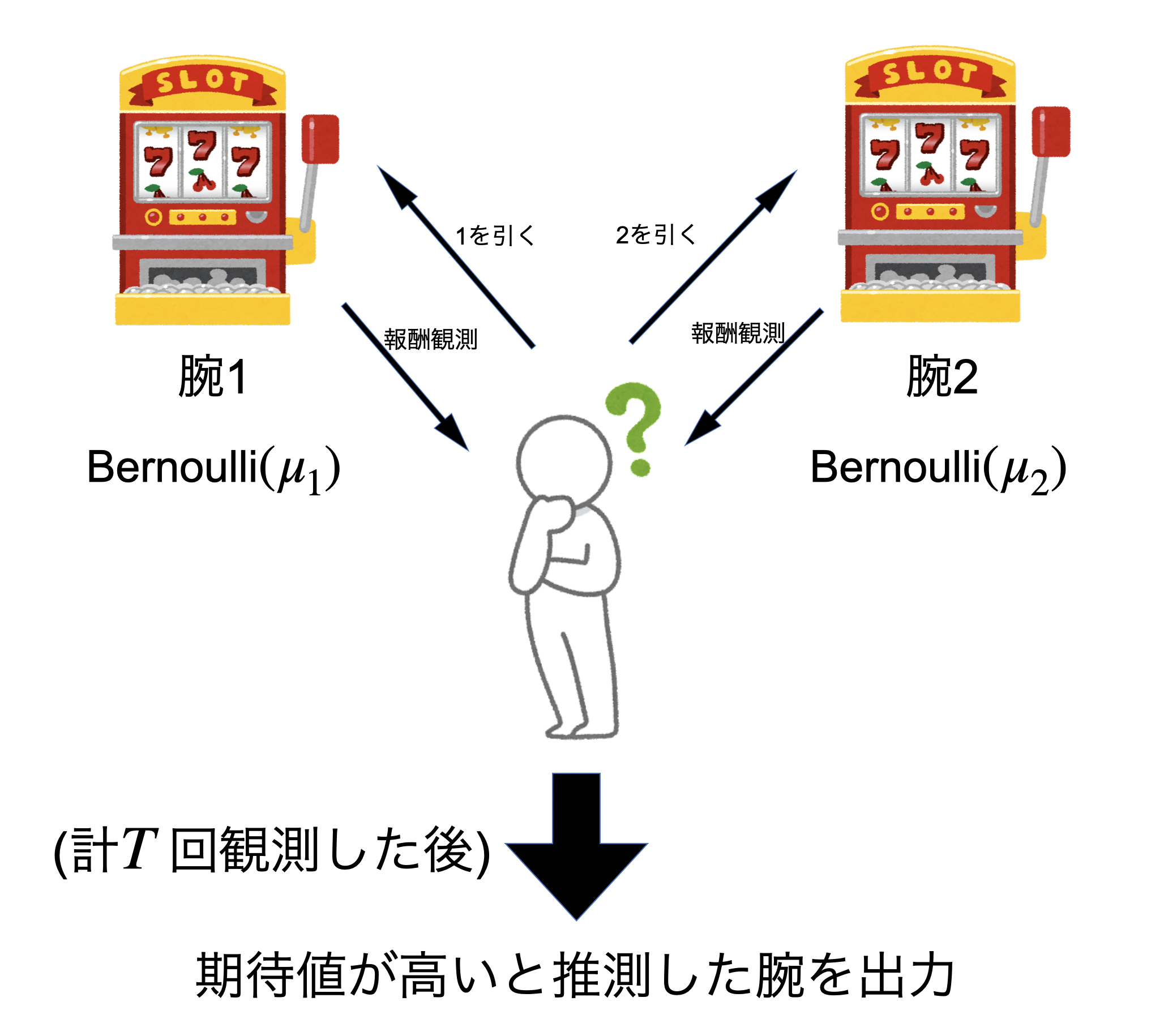
図1 ベルヌーイ報酬下の二腕固定予算最適腕識別問題の概略図。

各腕\(k \in \{1,2\}\)に対して、\(\mu_k \in (0,1)\)をその腕の期待値とします。当然、アルゴリズムは\(\bmu:= (\mu_1, \mu_2)\)の値について未知であるとします。最適腕は一つだけである、つまりは\(\mu_1 \neq \mu_2\)と仮定し、そのような腕の期待値の全組み合わせを\(\Lambda =\{\bmu \in (0,1)^2 : \mu_1 \neq \mu_2\} \)とします。固定予算最適腕識別問題としてA/Bテストを捉えた場合、アルゴリズムはサンプリングルール、および決定ルールの二つの要素で構成されます。サンプリングルールでは各\(t=1,2,\ldots,T\)ごとに、観測する腕\(A_t\)を過去の観測情報を元にして決めます。決定ルールは\(T\)回の観測が終了した後に、過去の観測情報を元に出力する腕\( \hat{\imath} \in \{1,2\}\)を決めます。期待値\(\bmu\)下での最適腕を\(1(\bmu) = \argmax_{k=1,2}\mu_k\)と表記します。今回の研究では、出力した腕が最適腕でない確率、つまりは誤り確率: $$p_{\bmu, T}:=\PP_{\bmu}\left[\hat{\imath}\neq 1(\bmu)\right]$$がなるべく小さくなるような手法について考察を行いました。

静的なアルゴリズムについて

この問題に対して適用できるシンプルなアルゴリズムとして、腕1と腕2を観測する量を事前に固定してサンプリングする、静的なアルゴリズムがあります。静的なアルゴリズムではサンプリングルールが観測情報に依存しません。特に、二腕の場合にはパラメタ\(x \in (0,1)\)にて腕2を観測する回数の割合を表現することによって、アルゴリズムを記述することができます。このとき、アルゴリズムは腕1を約\((1-x)T \)回、腕2を約\(xT \)回観測し、経験平均の値が大きな腕を出力します。

このような静的なアルゴリズムを固定予算最適腕識別問題に適用した際の(\(T \to \infty\)とする漸近的な)性能はよく知られています[1]。以下の関数を定義します:$$g(x, \bmu) := \min_{\lambda \in [0,1]} (1-x)d(\lambda ,\mu_1)+x d(\lambda,\mu_2).$$ここで、\( d(a,b) := a \ln (a/b) + (1-a)\ln ((1-a)/(1-b))\)は期待値が\(a\)および\(b\)であるベルヌーイ分布間のKLダイバージェンスです。以上の元で、静的なアルゴリズムの誤り確率は$$\lim_{T\rightarrow\infty} \frac{T}{\log(1/p_{\bmu,T})}=\frac{1}{g(x,\bmu)}$$という性質を満たします。この等式は、\(T\)が大きくなるにつれて、誤り確率 \(p_{\bmu,T}\) が \(e^{-g(x,\bmu)T}\) に近づき、\(T\)に対して指数的に減少することを示唆しています。\(g(x, \bmu)\)の値が大きいほど、\(p_{\bmu,T}\)の値は小さくなり、性能の良いアルゴリズムであることが分かります。特に、腕1と腕2を引く割合がともに\(1/2\)であるアルゴリズム(\(x=1/2\)としたアルゴリズム)を一様サンプリングと呼称し、その性能は$$\lim_{T\rightarrow\infty} \frac{T}{\log(1/p_{\bmu,T})}=\frac{1}{g(1/2,\bmu)}$$となります。

次に、任意の固定された\(\bmu \in \Lambda\)に対して、\(x\)の値を変化させることによって\(g(x, \bmu)\)を最大化することを考えます。\(g(x, \bmu)\)は\(x\)の関数として見ると強凹関数です。そのため、\(g(x, \bmu)\)には最大値を与える唯一の点\( x^*(\bmu)\)が存在します。また、関数\(g(x, \bmu)\)の形状および\( x^*(\bmu)\)は\(\bmu:=(\mu_1, \mu_2)\)の値によって変化することが分かります。この事実を図で見てみます。

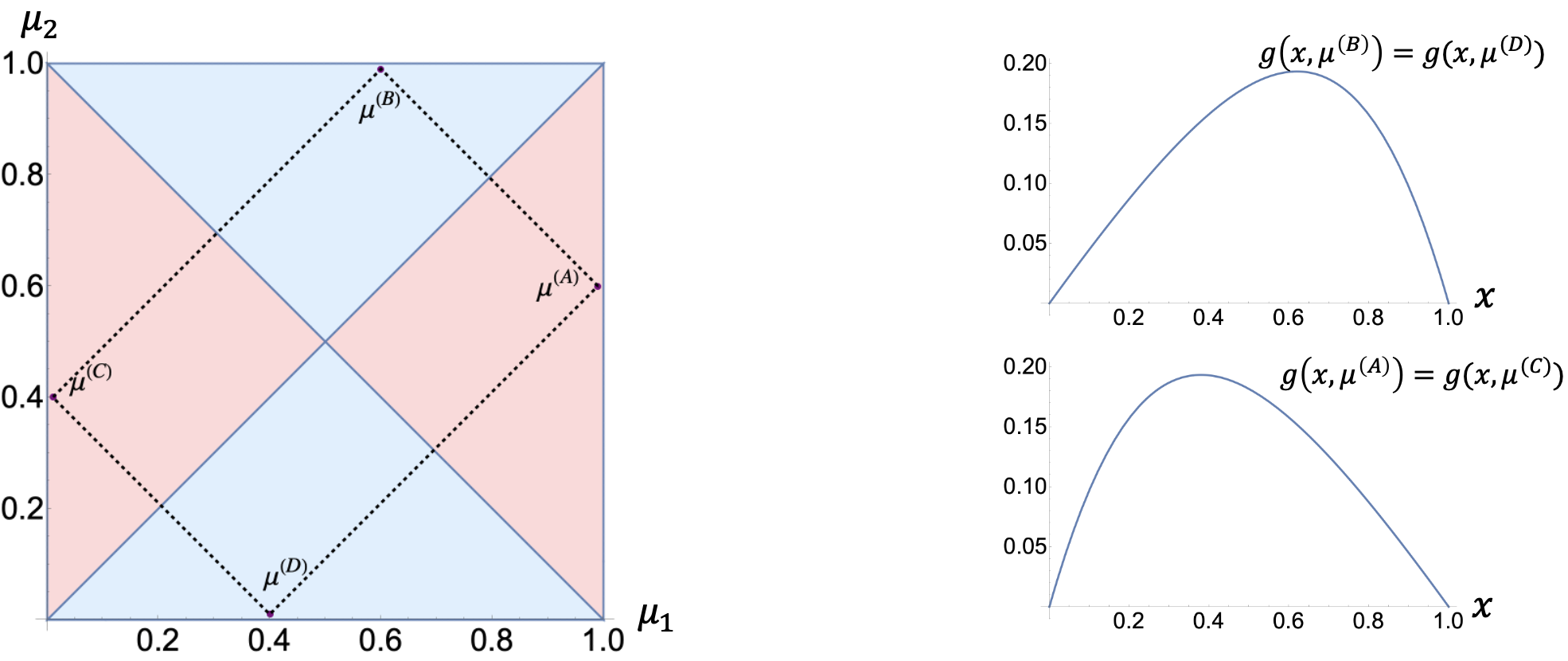
図2 関数\(g(x, \bmu)\)の性質の視覚化([2], Figure 2より)。(左)各期待値\(\bmu=(\mu_1, \mu_2)\)において、\(g(x, \bmu)\)を最大化する\(x^*(\bmu)\)の視覚化。\(x^*(\bmu)\)の値が1/2よりも大きい領域を青色で、 \(x^*(\bmu)\)の値が1/2よりも小さい領域を赤色で図示する。 (右) 代表的な\(\bmu\)における\(g(x, \bmu)\)の関数形の図示。

ほとんどの\(\bmu\)において、\(g(x,\bmu)\)を最大化するような腕2を引く割合\( x^*(\bmu)\)は1/2とは異なります。\( x^*(\bmu)\)の値さえ判明していれば、\(g(x^*(\bmu),\bmu)> g(1/2,\bmu)\)となり、静的なアルゴリズムの性能は一様サンプリングよりも良くなることが分かります。当然、そのような\( x^*(\bmu)\)の値は、本来未知である腕の期待値\( \bmu\)の値に依存しており、事前に最適な値を知ることはできません。しかしながら、最適腕識別のサンプリングルールでは過去の観測情報を用いて、動的に腕1と腕2を観測する量を変化させることが可能です。動的なサンプリングルールは性能向上にどの程度寄与するでしょうか。

主結果

論文における主結果を述べるために、一様サンプリングより良い、あるいは同等とされるアルゴリズムのクラスを定義します。あるA/Bテストのアルゴリズムが存在するとき、そのアルゴリズムの性能は任意の\( \bmu \in \Lambda\)に対して一様サンプリングより良いか、同程度の性能であってほしいと考えるのは自然です。そのため、一様サンプリングより良いアルゴリズムを、以下を満たすアルゴリズムとして定義します:$$\forall \bmu\in \Lambda, \quad \limsup_{T\rightarrow \infty} \frac{T}{\log (1/p_{\bmu,T})}\le \frac{1}{g(1/2,\bmu)}.$$ 本論文の主結果は次の定理となります。

定理: 任意の一様サンプリングより良いアルゴリズムに対して、以下が成り立つ:$$ \forall \bmu\in \Lambda,\quad \lim_{T\rightarrow \infty} \frac{T}{\log (1/p_{\bmu,T})}=\frac{1}{g(1/2,\bmu)}.$$

つまり、「任意の報酬の期待値\( \bmu \)に対して一様サンプリングよりも厳密に性能が良い」という性質を持ったアルゴリズムを構築することは不可能であることを示しています。これは、あるアルゴリズムの性能について、特定の\( \bmu \)に対して一様サンプリングよりも厳密に良い性能を示す場合でも、必ず別の\( \bmu’ \)が存在し、その\( \bmu’ \)の元では一様サンプリングよりも厳密に性能が悪くなることを示唆しています。

静的なアルゴリズムの例では、ある\( \bmu\)に対して最適な割合を設定した場合、別の\(\bmu’ \in \Lambda\)が存在し、その\(\bmu’\)においてアルゴリズムの性能が一様サンプリングよりも悪化します。上記の定理は、そのような性能悪化が任意の動的なアルゴリズムに対しても発生し、動的なサンプリングルールが性能向上に寄与しないことを明らかにしています。

証明について

ここでは定理の証明の流れについて、簡単に紹介したいと思います。証明ではまず、自然なアルゴリズムが持つ安定性という性質を発見し、それを利用しています。安定性の厳密な定義についてはここでは省略しますが、直観的には、安定性を持つアルゴリズムは期待値\( \bmu \)に対して対称的かつ連続的な挙動を示すアルゴリズムです。対称的とは、もし\( \mu_1 \approx \mu_2 \)であるならば、腕1と腕2とを引く割合がともに\(1/2\)に近くなるという性質です。連続的とは、もし二つの期待値\(\bmu\)と\(\bmu’\)が近い値(\(\bmu \approx\bmu’\))ならば、腕1と腕2とを引く割合が\(\bmu\)と\(\bmu’\)の間で近くなるという性質です。

さて、任意の安定性を持ったアルゴリズムに対して、その性能が一様サンプリングよりも同等か劣ることを、測度変換の議論[3]を用いて証明することができます。

定理¹: 任意の安定性を持つアルゴリズムに対して、以下が成り立つ:$$ \forall \bmu\in \Lambda,\quad \lim_{T\rightarrow \infty} \frac{T}{\log (1/p_{\bmu,T})}\ge\frac{1}{g(1/2,\bmu)}.$$

安定性を持たないアルゴリズムが「不自然な」アルゴリズムであることは、一様サンプリングよりもそのアルゴリズムの性能が悪化する\( \bmu’ \in\Lambda\)が存在することを証明することで示されます。

定理²: 任意の一様サンプリングより良いアルゴリズムは安定性を持つ。

上記の二つの定理から、主結果を得ることができます。

おわりに

本インターンシップは一様サンプリングよりも優れた性能を持つA/Bテスト手法を構築することをテーマに開始しました。しかし、研究を進める中でその困難さに直面し、最終的にはその非存在性を証明する方向へとシフトしました。活発で発見に満ちた議論は非常に楽しく、Po-Anさんをインターンとして迎えられたことは、メンターとして非常に喜ばしい経験でした。

取り組んだ問題は非常にシンプルな設定でありながら、未解決の問題が多く残されており、今後の発展が期待される分野です。AI Lab強化学習チームでは、このような強化学習の基礎的な研究にも積極的に取り組んでいます。

また、博士課程の学生を主な対象としたリサーチインターンや、共同研究なども募集しています。興味がありましたら、ぜひお気軽にご連絡ください。

参考文献

[1] Glynn, P. and Juneja, S. A large deviations perspective on ordinal optimization. In Proc. of the 2004 Winter Simulation Conference, 2004.

[2] Wang, P. A., Ariu, K., and Proutiere, A, On Universally Optimal Algorithms for A/B Testing. In Proc. of ICML, 2024.

[3] Garivier, A., Menard, P., and Stoltz, G. Explore first, exploit next: The true shape of regret in bandit problems. Mathematics of Operations Research, 44(2):377–399, 2019.

---

 

1, 2 非公式なstatementとなります。厳密な定理の内容は論文をご覧ください。↩ ↩