Blog
Synthetic Difference In Differenceの紹介
こんにちは、経済学チームの安井(@housecat442)です。
今日は最近気になっていた論文の一つであるSynthetic Difference In Differenceの内容を簡単に紹介します。
この論文は近年CS系のトップカンファレンスでも大活躍のSusan Atheyとその一派によって書かれており、タイトルもSynthetic ControlとDifference in Differenceの合わせ技を匂わせる非常に興味深いものです。
Synthetic Control(SC)は近年経済学において利用される事が増えてきた、因果効果を推定するための手法です。ちなみに今年のNeurIPSではこのSCを提案したAlberto AbadieによってSCのtutorialが行われます。
そんなSCを拡張した方法であるSynthetic Difference In Difference(SDID)をこの記事では簡単に紹介します。
ざっくりまとめると、この論文はSynthetic ControlとDifference in Differenceの合わせ技をDoubly Robust Estimatorのアイデアで実現し、さらに中で機械学習を使うという楽しい内容でした。
この記事では前提であるDifference In Difference(DID)とSynthetic Control(SC)の知識があるという想定で話を進めます。もしこれらの知識がない場合には、こちらの資料などを参考にされると良いと思います。
DIDとSCについて
まずDIDにおける因果効果の推定を思い出します。
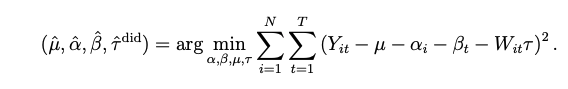
i: 観測対象
t: 時間
Y: outcome
α: 個人効果
β: 時間効果
μ: constant
W: 介入
τ: 因果効果
これは各観測対象の各時点での回帰モデルの二乗誤差を最小にしているということになります。
一方でSCは以下のような分析を行います。
まずある対象Nがある期間Tにおいて介入を受けるものとします。
そこでN以外で期間Tより前のYを使い、Nの期間Tより前のYをうまく予測できる方法を考えます。
これは以下のような重み付きの和で表す事が可能です。
![]()
そして期間Tにおいてこの重みを使って、N以外のデータからNのYを予測します。
Tより前の期間において、介入が行われていない時のNのYを予測する重みなので、期間Tで介入が行われない場合のNのYを予測している事になります。
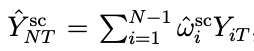
よって、この予測値と実際に介入による影響を受けている結果の差を介入の因果効果と考える事ができます。
![]()
SDIDについて
SDIDはこれに対して以下のような形になります。
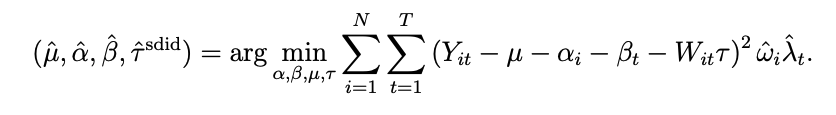
これは一見DIDとほぼ同じに見えますが、実際にはSCで見たような重みに加えてλという新しい重みがかけられています。
つまり、これら二つの重みを掛けた何かしらの新しい重みを使って、重み付きの二乗誤差の最小化を行う事で介入の因果効果を推定しているという事になります。
この時λはNを除く観測対象のT以外のサンプルから、Tのサンプルを予測できるような重みとして得られたものになります。
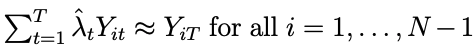
また、これらの重みを得る際にL2(ridge)正則化を用いる事も可能となっているそうです。
さて、SDIDの重み付きの誤差を見てDoubly Robust Estimator(DR)を思い出した人もいるかと思います。
実はこのSDIDもDRと同様にdouble robustnessと呼ばれるメリットを享受する事が可能です。つまり、回帰モデルか重みのどちらか一方のみが間違っているような場合でも因果効果に関しては一致性が担保されます。
SDIDの実験
この論文ではSCの紹介論文で使われたデータを利用してSDIDの性能を検証しています。
SCおよびSDIDは”介入を受けたサンプルの介入を受けなかった結果を正しく予測できるか?”が非常に重要となります。
よって、ここでは介入を受けてない期間のデータのみを使い、その最後の期間をTとし、任意の観測対象をNとして扱います。
こうする事で、実際に予測する対象が介入を受けない対象となるために、実際の正解データを得る事が可能になります。
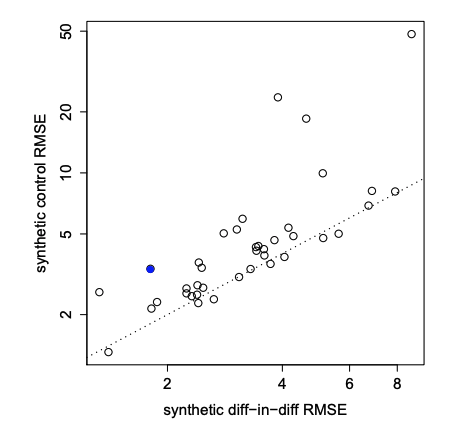
この図がSCとSDIDの予測誤差(RMSE)をプロットした図です。
点線が傾きが1の線なので、線よりも上側にある点はSCの方が誤差が大きいという事になります。
これを見るとほぼ全ての点が線より上側にあるため、SDIDの性能がかなり高いであろう事がわかります。
また、このデータではカリフォルニア州が介入(禁煙キャンペーン)を受ける州で、青くハイライトされています。よって効果の推定において重要になるカリフォルニア州においても誤差が小さくなる事がわかります。
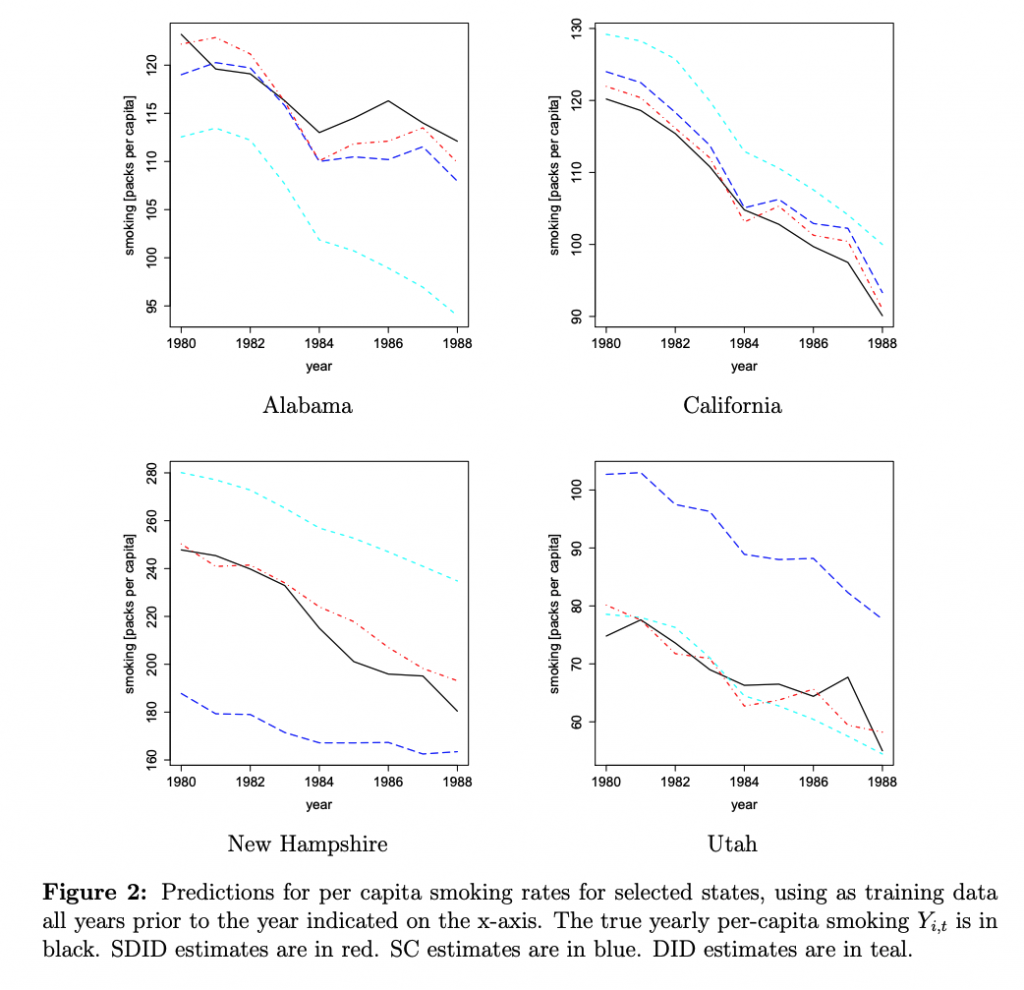
また、複数の年にまたがって予測と実際の値をプロットした図も乗っています。
黒い線が実際の値で、赤の点線がSDID、青い点線がSC、水色の点線がDIDです。
これを見てもやはりSDIDが良さそうな結果となっています。
感想とか
試す事自体はかなり簡単な手法なので、とりあえず使ってみようと思いました。
また、共編量が高次元の設定であれば、回帰の部分でDouble Machine Learningを導入する事が可能な気もしたのですがどうなのでしょうか?
Author
