Blog
人間を超えたゲームAIの基盤となった経済学 〜ナッシュ均衡とその計算アルゴリズム〜
AI Lab 経済学チームの森下(@GotaMorishita)です.
今年7月に複数人のポーカーで圧勝したポーカーAI, Pluribus[1]が話題になりました. Pluribusやその元となったLibratus[2]で用いられた理論は, ミクロ経済学の一分野であるゲーム理論のナッシュ均衡でした. ポーカーを展開型ゲームとして定式化し, そのゲームのナッシュ均衡を求め, それを最適戦略としたのです.
ナッシュ均衡を求めるアルゴリズムはコンピューターサイエンスでは盛んに研究されており, LibratusやPluribusではCounterfactual Regret Minimization (CFR)と呼ばれる展開型ゲームのナッシュ均衡計算アルゴリズムを応用したものが使われています[3]. 弊ブログでも, 先日, CFRアルゴリズムを花札「こいこい」に適用させた例を紹介しました(こちら).
このブログでは, CFRアルゴリズムの元となったRegret Matchingと呼ばれる標準型ゲームの均衡計算アルゴリズムを解説し, 実験でじゃんけんゲームに対してこのアルゴリズムを適用させた例を紹介します.
Regret Matching アルゴリズム
ポーカーなどの状態数が膨大な不完全情報ゲームは, 長年, ゲームAIの分野では未解決問題の1つとして残っていました. そんな中, HartとMas-Colellが, Regret Matchingと呼ばれるナッシュ均衡を求めるためのヒントとなるアルゴリズムを経済学のトップジャーナルであるEconometricaで2000年に発表しました[4].
このアルゴリズムが提案されたことを契機にポーカーAIの攻略が一気に進みました. コンピュータサイエンスの一分野に革命をもたらしたアルゴリズムが, 純粋な経済学のジャーナルで発表されたことは非常に感慨深いと思いました.
さて, 簡単にこのアルゴリズムを説明すると, 過去のプレイのリグレット, つまり, 違う行動をしておけばよかったという後悔を定量化し, それを減らすように戦略を変化させていき, ナッシュ均衡戦略に近づけていくアルゴリズムになります.
この章では, アルゴリズムを説明する前に, ゲーム理論のいくつかの基本的な用語と定義を紹介し, 最適な戦略のための解の概念であるナッシュ均衡について説明します. そのあとRegret Matchingアルゴリズムについて解説し, 最後にRegret Matchingアルゴリズムを使ってじゃんけんゲームのナッシュ均衡を求める実験の結果を示します.
ナッシュ均衡とは
ポーカーなどのゲームにおいて, 最適または完全にプレイするとはどういうことでしょうか. 勝ち負けが相手のプレー次第であることを考えると, この問い自体に何か意味があるでしょうか. ゲームAIを作る上で, 最適な戦略というものを定義する必要があります.
その答えの1つがナッシュ均衡と呼ばれるゲーム理論における解概念です[6]. ナッシュ均衡とは, 複数人が関わるシステムで, お互いの戦略を予測しながら自らの利益を最大化するように戦略を決めるときに, どのような行動が現れるかを示すモデルの1つです. 特にプレイヤーが2人で利得の和が常に0である2人ゼロサムゲームと呼ばれるゲームのクラスのナッシュ均衡は理論的に非常にうれしい性質があります. ボードゲームの多くはこのクラスに属するので, ゲームAI界では非常に重宝されています.
それでは数学的にナッシュ均衡を定義するためにいくつかのゲーム理論の基本用語を定義します. まず標準型ゲームを \((N, A, u)\)として定義します.
- \(N = \{1, \dots, n\}\)は\(n\)人の有限集合.
- \(S_i\)はプレイヤー\(i\)の行動の有限集合.
- \(A = S_1 \times \dots \times S_n\)は全てのプレイヤーの同時行動の全ての組み合わせの集合. 各組み合わせを行動プロファイルを呼びます.
- \(u\)は行動プロファイルから各プレイヤーの利得のベクトルを返す関数です. \(u_i\)はプレイヤー\(i\)の利得を表します.
標準型ゲームとは, 一回きりのゲームで, 各プレイヤーが一回だけ行動を選択し, それらの行動プロファイルから得られる利得を得て終了します.
通常, 以下の図のように標準型ゲームは\(n\)次元のテーブルで, 表現されます. この図では2人のプレイヤーがいて, 各プレイヤーは同じ行動空間\(S_1 = S_2 = \{R, P, S\}\)を持っています. ここで, \(R, P, S\)は, グー(Rock), パー(Paper), チョキ(Scissors)を表しています.

図1 じゃんけん標準型ゲーム([5]から引用)
行と列は各プレイヤーの行動が書かれており (図ではR, P, S), 各行動プロファイルでもらえる利得のペアがテーブルの中に書かれています. 図では, 各プレイヤーは同じ行動空間を持っているため対称的ですが, 各プレイヤーが別の行動空間を持っていても構いません.
それぞれ, プレイヤー\(1, 2\)の行動は行, 列に書かれています. 各プレイヤーの行動の組み合わせの空間\(A\)は, このじゃんけんゲームの例では, \(A = \{(R, R), (R, P), \dots, (S, P), (S,S)\}\)となります.
上のテーブルから具体的に利得を計算してみましょう. プレイヤー\(1\)が行動\(R\)をとり, プレイヤー\(2\)が行動\(P\)を取った時のそれぞれの利得は, それぞれ\(u_1(R, P) = -1\), \(u_2(R, P) = 1\)となります.
またどの行動をとるかを決定的に決める必要はなく, 確率的にどの行動をとるかという戦略も考えることができます. そのような戦略を混合戦略と呼びます. 混合戦略は\(\sigma\)で表し, その戦略において, プレイヤー\(i\)が行動\(s \in S_i\)を取る確率を\(\sigma_i(s)\)と書きます.
確率的に行動を決めたときの利得は期待値を用いて計算します. 具体的には以下のように計算します.
$$ u_i(\sigma_i, \sigma_{-i}) = \sum_{s \in S_i}\sum_{s’ \in S_{-i}} \sigma_i(s)\sigma_{-i}(s’)u_i(s, s’).$$
ここで, 経済学の慣習で, プレイヤー\(i\)以外のプレイヤーは\(-i\)を用いて表します.
次に相手の混合戦略\(\sigma_{-i}\)に対して最適応答\(BR(\sigma_{-i})\)というものを定義します. これは相手が混合戦略\(\sigma_{-i}\)に対して, もっとも利得が高くなるような自身の戦略の集合です. 数学的に表すと,
$$BR(\sigma_{-i}) = \mathop{\rm arg~max}\limits_{\sigma_i} u_i(\sigma_i, \sigma_{-i}).$$
この最適応答を用いてナッシュ均衡を定義します.
全てのプレイヤーが他のプレイヤーの戦略に対して最適応答の戦略を取っている時, その戦略の組み合わせをナッシュ均衡と呼びます. ナッシュ均衡戦略を\(\sigma^*\)とし, 数式で表すと,
$$ \forall i \in N \quad \forall \sigma_i \in \Delta (S_i) \quad u_i(\sigma_i^*, \sigma_{-1}^*) \geq u_i(\sigma_i, \sigma_{-1}^*)$$
相手がナッシュ均衡戦略に従っている限り, 自分がナッシュ均衡以外の他の戦略を取ったとしても利得をあげることができないことを意味します. したがって, ナッシュ均衡戦略はゲームにおいて実現しうる戦略と言えます.
数式と説明ばかりで, わかりにくいと思うのでここで1つ例を出します. 以下の図で示した男女のジレンマと呼ばれる標準型ゲームを考えます.
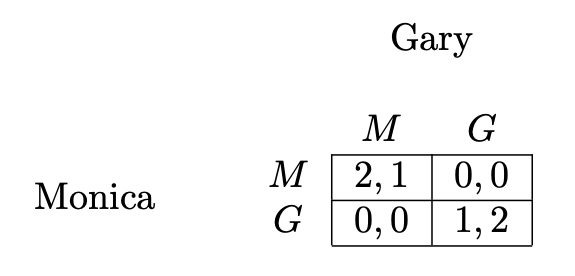
図2 標準型ゲームである男女のジレンマゲーム([5]から引用)
ストーリーはこうです.
男女のカップルがおり, 男の子のGaryは, サッカーの試合(G)を見にいきたいと思っています. 一方で, 女の子のMonicaは, 映画(M)を見にいきたいと思っています. お互いに好きなので, 離れ離れで行くのは嫌だと考えています. ですから, もしお互い別々の選択をしてしまった場合, お互いの利得は\(0\).
もし, 2人でサッカーを見に行った場合は, 見たかったサッカーに行けてGaryは利得2, 映画の方が良いが一緒にいれるのでMonicaは利得1を得ます. 逆に2人で映画を見に行った場合, サッカーの方が良いが一緒にいれるのでGaryは利得1, 映画に行きたかったMonicaは利得2を得ます.
さて, このゲームにおけるナッシュ均衡は何でしょうか. Monicaの立場になってGaryの各行動に対する最適応答を考えてみましょう. もしGaryがサッカーに行く\((G)\)という行動を取るとしたら, Monicaのその行動に対する最適応答は\(G\)です. なぜならば, \(u_{Monica}(G, G) = 1 \gt 0 = u_{Monica}(M, G)\)だからです.
一方で, Garyが映画に行くという行動\((M)\)を取るとしたら, Monicaのその行動に対する最適応答は\(M\)です. なぜならば, \(u_{Monica}(M, M) = 2 \gt 0 = u_{Monica}(G, M)\)だからです.
今度はGaryの立場になって考えます. 対称性からGaryも同じで, Monicaの\(G\)に対する最適応答は\(G\)で, \(M\)に対する最適応答は\(M\)です. よって, \((G, G)\)と\((M, M)\)がナッシュ均衡になります.
確率的な戦略, つまり, 混合戦略の範囲まで考えるともう1つナッシュ均衡が存在します(ほとんどすべての有限ゲームはナッシュ均衡を奇数個持ちます[7]).
混合戦略のナッシュ均衡の求めるには, 少しコツが必要です. 以下の事実を用います.
(★) 相手が混合戦略の範囲のナッシュ均衡をとっている場合は, ナッシュ均衡戦略で確率が\(0\)でないどの行動を取ったとしても同じ利得しか得られない ([8]のPropostion8.D.1).
もう一度, Monicaの立場になって考えてみましょう. もしGaryが確率\(p \in (0, 1)\)で, 映画\((M)\)に見に行き, 確率\(1-p\)でサッカー\((G)\)に見に行くという混合戦略\(\sigma_{Gary}\)を取るとします.
このとき, (★)を用いて考えると, ナッシュ均衡であるような\(p\)は,
$$u_{Monica}(M, \sigma_{Gary}) = u_{Monica}(G, \sigma_{Gary})$$
を満たします.
\(u_{Monica}(M, \sigma_{Gary}) = 2p, u_{Monica}(G, \sigma_{Gary}) = 1 – p\)であるから, \(p = \frac13\)となります. 対称性からMonicaのナッシュ均衡戦略\(\sigma_{Monica}^*\)は, \(\sigma_{Monica}^*(G) = \frac13, \sigma_{Monica}^*(M) = \frac23\)となります.
従って, ナッシュ均衡戦略は\(\big((\frac23, \frac13), (\frac13, \frac23)\big)\)となります.
Regret Matchingとは
まずリグレットについて定式化します.
リグレットとは, 一言で言うと過去の行動における後悔の度合いを他の行動と比べて定量化したものです. まずじゃんけんゲームを例にして, 具体的にリグレットを説明します.

図3 じゃんけん標準型ゲーム(再掲)
上の図のゲームが一度行われたとします. その結果, プレイヤー\(1\)がパー\((P)\)で, 相手がチョキ\((S)\)でした.
この時, プレイヤー\(1\)の利得は\(u_1(P, S) = -1\)です.
もし仮にチョキ\((S)\)を出していれば, あいこになって利得は\(u(S, S) = 0\)でした. つまり, チョキ\((S)\)を出していれば相対的に\(u_1(S, S) – u_1(P, S) = 0 – (-1) = 1\)嬉しかったことになります. これをチョキ\((S)\)に対するリグレットと呼びます.
同様に, グー\((R)\)に対するリグレットは, \(u_1(R, S) – u_1(P, S) = 2\)になります.
同じ行動に対しては, 利得が変化しないため, パー\((P)\)に対するリグレットは\(0\)です. もしリグレットが負になった場合, \(0\)として扱います.
さて, このリグレットはどのように使われるのでしょうか. リグレットは次のゲームの戦略を決めるために使われます. 具体的には, 次のゲームは, 各戦略のリグレットの比率ごとに確率を割り振った混合戦略をプレイします.
上のじゃんけんの例では, \(R, P, S\)のリグレットは, それぞれ\(2, 0, 1\)でした. したがって, リグレットの比率をもとに次の混合戦略を決めると\(\big(\frac{2}{1+2}, 0, \frac{1}{1+2}\big)\)となります. このプロセスのことをRegret Matchingと呼びます.
この混合戦略をもとにもう一度プレイします.
このとき, 自分がグー\((R)\) (確率\(\frac23\))で, 相手がパー\((P)\)だとします.
もう一度, このゲームにおけるリグレットを計算します. すると, \(R, P, S\)のリグレットは, それぞれ\(0, 1, 2\)となります. このとき, 次のゲームにおける混合戦略を考える際, リグレットの比率を用いるのですが, 今までのリグレットの累積を使います. つまり, 以前のリグレットに現在のゲームのリグレットを足して累積のリグレットの比率を用いて, 混合戦略を考えます.
今の例では, \(R, P, S\)の累積リグレットはそれぞれ, \(2 + 0 = 2, 0 + 1 = 1, 1 + 2 = 3\)です. よって, 次のゲームにおける混合戦略は, \(\big(\frac13, \frac16, \frac12\big)\)となります.
相手も自分もRegret Matchingを使って戦略を更新していくと, 平均戦略(各イテレーションにおける戦略の平均)の組み合わせは相関均衡に収束することが知られています[4]. つまり, self-playを用いれば, ある種の解の戦略が得られるということです. self-playとはシミュレーションで自分と同じ戦略を持った架空のプレイヤーとプレイすることです.
今までナッシュ均衡の話をしていたのに, 突然, 相関均衡が出てきましたが, ナッシュ均衡よりちょっと弱い解概念と思っておけば差し支えないです.
もし気になる方は,[4, 9, 10]が詳しいです.
じゃんけんにおける実験
上で紹介したじゃんけんゲームに対して, Regret Matchingアルゴリズムを適用させて, 実際に均衡に到達するかを検証しました. 実際のコードは, ここにおいてあります.
じゃんけんゲームのようなある条件を満たす2人ゼロサムゲームにおいては, 相関均衡とナッシュ均衡は一致します. したがって, Regret Matchingアルゴリズムを用いれば, ナッシュ均衡を求めることができます. 今, じゃんけんゲームのナッシュ均衡は\(\big(\frac13, \frac13, \frac13\big)\)です. グラフに示されているのは, ナッシュ均衡戦略とRegret Matchingにおける戦略の各行動の確率の絶対値の差の和です.
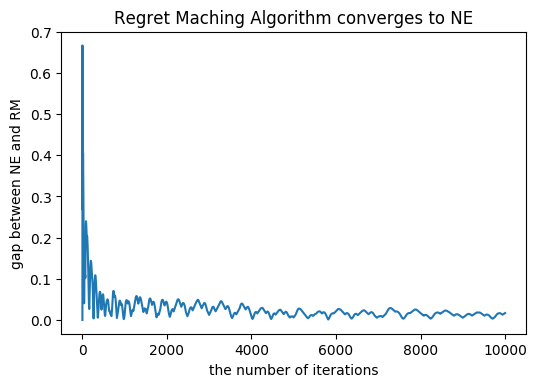
図4 平均戦略とナッシュ均衡戦略の差のグラフ
前半では大きく差がぶれていますが, 更新が進むにつれて, 差が縮まっていくことがわかると思います. 2000回目あたりで, 差がほぼない状況で, 収束していると言えます. 実際に混合戦略をみてみると, ほぼ\(\frac13\)になっていました.
またColonel Blottoと呼ばれるゲームで, 行動は21個あり, 簡単にナッシュ均衡が求まらないゲームについても実装してあるので, 試しに動かしてみると面白いと思います.
終わりに
今回はゲーム理論の基本をおさらいして, 標準型ゲームの均衡計算アルゴリズムであるRegret Matchingについて解説を書きました.
次回は, 展開型ゲームのナッシュ均衡の計算アルゴリズムCounterfactual Regret Minimizationのまとめを書いてみたいと思います.
参考文献
[1] Brown, Noam and Tuomas Sandholm. “Superhuman AI for multiplayer poker.” Science 365 (2019): 885-890.
[2] Brown, Noam and Tuomas Sandholm. “Safe and Nested Endgame Solving for Imperfect-Information Games.” Proceedings of the AAAI workshop on Computer Poker and Imperfect Information Games (2017).
[3] Zinkevich, Martin et al. “Regret Minimization in Games with Incomplete Information.” NIPS (2007).
[4] Sergiu Hart and Andreu Mas-ColellA. “Simple Adaptive Procedure Leading to Correlated Equilibrium.” Econometrica Vol. 68, No. 5 (Sep., 2000), pp. 1127-1150
[5] Neller, Todd W. and Marc Lanctot. “An Introduction to Counterfactual Regret Minimization.” (2013).
[6] Nash, John F.. “Equilibrium Points in N-Person Games.” Proceedings of the National Academy of Sciences of the United States of America 36 1 (1950): 48-9 .
[7] Robert Wilson. “Computing Equilibria of N-Person Games.” SIAM Journal on Applied Mathematics Vol. 21, No. 1 (Jul., 1971), pp. 80-87
[8]A. Mas-Colell, Green, J. R., and M. Whinston. “Microeconomic Theory.” New York: Oxford University Press, (1995).
[9] Aumann, Robert. “Correlated Equilibrium as an Expression of Bayesian Rationality.” Econometrica. 55 (1) (1987): 1–18.
[10] Francoise Forges. “Correlated Equilibrium in Two-Person Zero-Sum Games.” Econometrica, 1990, vol. 58, issue 2, 515
Author
