Blog
論文解説「Lookahead Optimizer: k steps forward, 1 step back」
AI Lab AutoMLチームの野村です.
本稿では,最近読んだ論文「Lookahead Optimizer: k steps forward, 1 step back」[1] について,解説を行いたいと思います.
こちらの論文は今月開催されるNeurIPSに採択されています.
Deep Neural Networksのための最適化手法というとstochastic gradient descent (SGD) やAdamが有名かと思いますが,こちらの論文ではこれらの最適化手法と提案手法を組み合わせることでより高い性能を示すことに成功しています.
まず最初に,近年のSGDからの拡張には,大きく2通りの方向性があります:
(1) 学習率適応 : AdaGrad, Adamなど
(2) 加速法 : Polyak heavyball, Nesterov momentumなど
これらの手法では過去の勾配を利用して効率良い探索を可能にしていましたが,ハイパーパラメータチューニングに大きなコストがかかることが問題となっていました [2].
今回の論文では,上記の問題に対処した手法 Lookahead optimizer を提案しています.
Lookaheadという名前のとおり,過去の勾配を使うのではなく,先を見据えた更新則を導入しています.
具体的には,通常のoptimizer (SGDやAdamなど) によって重みパラメータを更新します.
これらのパラメータを “fast weights” を呼びます.
次に,これらの “fast weights” を参考に,”slow weights”と呼ばれる,実際に評価に用いる重みパラメータを更新します.
つまり,これまでのoptimizerは”fast weights”の更新で終わっていましたが,Lookahead optimizerはこの更新を参考にした上で本当のパラメータ (slow weights) を更新するというわけです.
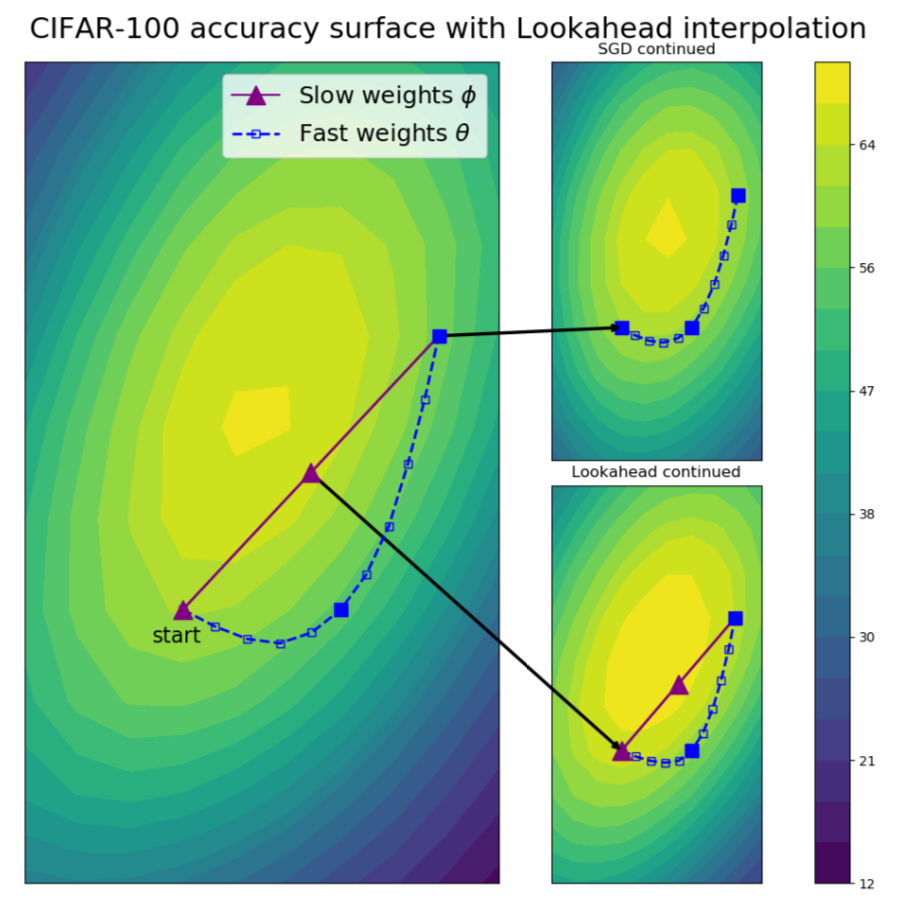
Ref. [1] : 青の点線がfast weights, 紫の点線がslow weightsを表す.
こちらの図は,更新の過程を2次元空間に射影したものです.
“fast weights”によって数ステップ更新された重みを用いて,”slow weights”の更新方向を決定している様子を観察することができます.
最終的なアルゴリズムは非常にシンプルです.
まず,inner loopにて,”fast weights”を以下の式で\(k\)回更新します.ここで\(k\)はouter loopとの同期間隔を決定するユーザパラメータ,Aはoptimizer,Lは損失関数です.
$$\begin{align}
&\theta_{t,i} \gets \theta_{t,i} + A (L, \theta_{t,i-1}, d),\\
&d\ {\rm is\ minibatch\ of\ data\ sampled\ from\ data\ distribution}\ \mathcal{D}.
\end{align}$$
inner loopでの”fast weights”の更新を\(k\)回行う度に,outer loopにて”slow weights”の更新を以下の式で行います.
ここで,\(\alpha\)はステップサイズです.
$$\begin{align}
\phi_t \gets \phi_{t-1} + \alpha (\theta_{t,k} – \phi_{t-1}).
\end{align}$$
それでは,上式に現れるステップサイズ\(\alpha\)はどう決定すれば良いでしょうか?
論文では,loss functionをquadraticな形式で表せると仮定した上で(つまり,\(L(x) = \frac{1}{2}x^{\top} A x – b^{\top} x\)),lossを最小にする最適な\(\alpha^{*}\)を以下で導出しています.
これは\(\alpha\)で微分した結果から直ちに導出されます.
$$\begin{align}
\alpha^{*} &= {\rm argmin}_{\alpha} L(\theta_{t,0} + \alpha (\theta_{t,k} – \theta_{t,0})) \\
&= \frac{(\theta_{t,0} – \theta^{*})^{\top} A (\theta_{t,0} – \theta_{t,k})}{(\theta_{t,0} – \theta^{*})^{\top} A (\theta_{t,0} – \theta_{t,k})},
\end{align}$$
where \(\theta^{*} = A^{-1} b\) minimizes the loss.
しかしながら,DNNなどの問題では非常に高次元となるため,\(A\)を推定することは一般的に難しいです.
そこで,論文では,対角近似した場合にうまくいくような\(\alpha\)についても説明しています.
ただ,論文内の実験では,今回紹介した最適な\(\alpha\)ではなく,固定値(例えば,\(\alpha = 0.5\)など)を用いています.
この理由としては,
- 収束曲線は似ているが,汎化性能は固定した方が良い
- 対角近似に必要なempirical Fisherの推定などが必要なくなり,メモリや計算コストの点でメリットがある
ということが述べられています.
次に,Lookaheak optimizerとSGDの挙動の違いを,varianceの観点から議論します.
ここでは,Schaulら [3]も用いている,ノイズも考慮した以下のquadratic modelを仮定しています.
$$\begin{align}
\hat{\mathcal{L}}(x) = \frac{1}{2}(x – c)^{\top} A (x – c),
\end{align}$$
with \(c \sim \mathcal{N}(x^{*}, \Sigma)\).
ここで,\(A\)と\(\Sigma\)は対角行列であり,\(x^{*} = 0\)であると仮定します.
また,\(A\)と\(\Sigma\)の要素をそれぞれ\(a_i\)と\(\sigma_i^2\)と表記します.
ここで,\(0 < \gamma < 2/L (, L = \max_i a_i) \)を(slow weightsに対してとは限らない)学習率とします.
上記のnoisy quadratic modelに対して,SGDとLookahead + SGDは,期待値としては\(0\)に収束し,分散は以下の固定点に収束することが示されています.
$$\begin{align}
V_{SGD}^{*} &= \frac{\gamma^2 A^2 \Sigma^2}{I – (I – \gamma A)^2},\\
V_{LA}^{*} &= \frac{\alpha^2 (I – (I – \gamma A)^{2k})}{\alpha^2 (I – (I – \gamma A)^{2k}) + 2\alpha (1 – \alpha) (I – (I – \gamma A)^{k})} V_{SGD}^{*}.
\end{align}$$
ここで,\(V_{LA}^{*}\)の最初の項は\(\alpha \in (0, 1)\)に対して厳密に\(1\)より小さくなるので,\(V_{LA}^{*}\)は\(V_{SGD}^{*}\)より小さくなることが保証されます.
実験では,
- CIFAR-10/100
- ImageNet
- neural machine translation
- Penn Treebank
などの,画像から言語まで様々なデータセットにおける実験が行われているのですが,
SGDがハイパーパラメータに対して敏感であるのに対し,Lookahead optimizerはロバストであることが強調されています(以下参照).
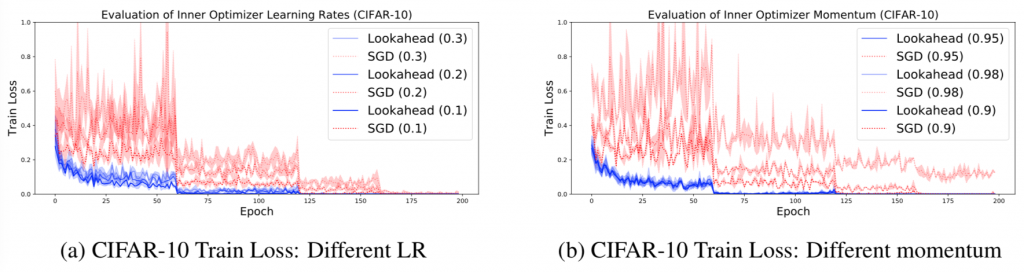
Ref. [1] : SGDが学習率,モメンタム係数に対して敏感であるのに対し,提案手法Lookaheakはロバストなことが確認できる.
最後に
本稿では,比較的シンプルな操作でSGD,Adamの性能を向上させたLookahead optimizerについて紹介しました.
ハイパーパラメータのチューニングにおいても学習率は特に影響が強いので,今回の論文のような学習率の設定にロバストが手法が増えると安心して使える場面が増えるなと思いました.
著者によるコード(PyTorch, Tensorflow)もこちらに公開されているので,興味がある方はご覧ください.
References
[1] Michael Zhang, James Lucas, Jimmy Ba, and Geoffrey E Hinton. Lookahead optimizer: k steps forward, 1 step back. In Advances in Neural Information Processing Systems, pages 9593–9604, 2019.
[2] Gregoire Montavon, Genevieve Orr, and Klaus-Robert Muller. Neural networks: tricks of the trade, volume 7700. springer, 2012.
[3] Tom Schaul, Sixin Zhang, and Yann LeCun. No more pesky learning rates. In International Conference on Machine Learning, pages 343–351, 2013.
Author
