Blog

Research

2020.1.28

Gradient Reversal LayerではじめるPyTorchカスタム関数

Gradient Reversal Layer

AI Labの大田（@ciela）です。近頃の機械学習モデルにおいて、敵対的な学習を行うことで有名なのは生成器ネットワークと識別器ネットワークが互いに競い合うように学習するGenerative Adversarial Networks (GAN) かと思いますが、転移学習の一種であるドメイン適応においても敵対的な学習を行うモデルが提案されています。ドメイン適応の目的は、学習データ（ソースドメイン）とテストデータ（ターゲットドメイン）におけるデータ分布が異なるような状況においてもうまく機能するようなモデルを学習することです。ターゲットドメインのデータ分布をソースドメインのデータ分布に近づけるように学習するのですが、これを敵対的なやり方で行うというわけです。ドメイン適応自体についてはAI Labの安井もブログ記事を書いていますのでこちらも併せてお読みいただければ幸いです。

Ganinらは教師なしドメイン適応モデルであるDomain-Adversarial Neural Network (DANN)を提案しており、異なる画像表現を持つ画像データセットでの有効性を示しています。

Domain-Adversarial Training of Neural Networks [Ganin, JMLR2016]

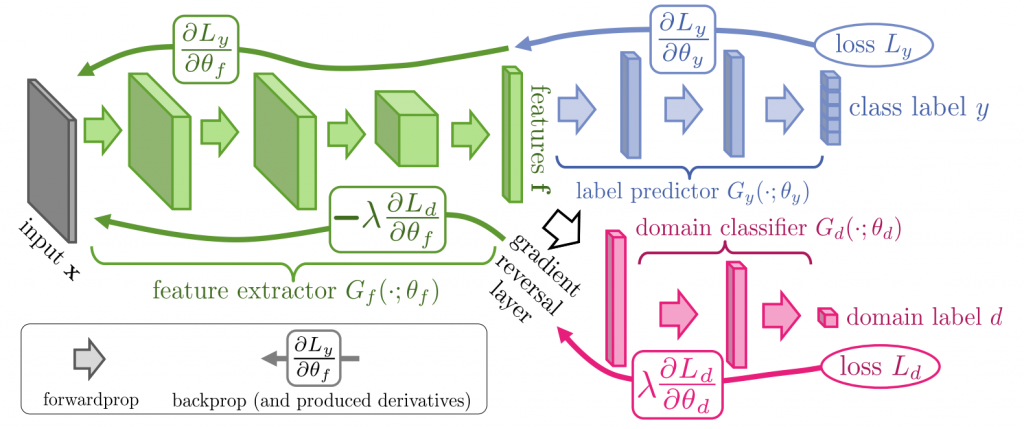
論文よりDANNのアーキテクチャ図

上図を参照してみると特徴抽出CNNを経たあとクラス分類とドメイン分類の2つのサブネットワークに分岐していますが、ドメイン分類のサブネットワークにおいてはGradient Reversal Layer (GRL)という層を通していることが分かります。この層は誤差逆伝搬時にのみ前段の層へ伝わる勾配の符号を反転させるのですが、これによってクラス分類能力を高めつつもドメイン分類能力は落とすという敵対的な学習が行われます。その結果、前段の特徴抽出層においてドメイン不変性のある特徴獲得能力が向上するという仕組みになっています。

このGRLはGANの学習にも利用できます。生成器と識別器を交互に学習させる実装が主流かと思いますが、下記の記事においてはGRLを利用して生成器へ伝搬される勾配を反転するだけで目的関数がシンプルになり実装が簡単になるという利点が紹介されています。

Gradient reversal layerを使うとGANの実装が簡単になる – Qiita

さて、今回は私もドメイン適応モデルを構築する機会があり、ベースモデルとしてDANNを実装する上でGRLについても理解・利用する必要性が出てきました。普段使いしているDNNフレームワークはPyTorchなのですが、2020年1月現在の最新版である1.4.0にはこのGRLの実装は含まれていないようです。これまで活性化関数などを独自実装した経験がなかったこともあり、本記事ではPyTorchでGRLの実装を行い実際に簡単なモデルに組み込んで挙動を確認してみたいと思います。

PyTorchでのGRL実装

PyTorch において、誤差逆伝播時に勾配情報を制御するためには torch.autograd.Function クラスを利用して独自関数を定義することになるかと思います。

PyTorch: Defining New autograd Functions — PyTorch Tutorials 1.4.0 documentation

上記ページを参考にして定義してみた場合、下記のようになります。

class GradientReversalFunction(torch.autograd.Function):
    
    @staticmethod
    def forward(ctx, input_forward: torch.Tensor, scale: torch.Tensor) -> torch.Tensor:
        ctx.save_for_backward(scale)
        return input_forward

    @staticmethod
    def backward(ctx, grad_backward: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        scale, = ctx.saved_tensors
        return scale * -grad_backward, None

class GradientReversalFunction(torch.autograd.Function):

@staticmethod

def forward(ctx, input_forward: torch.Tensor, scale: torch.Tensor) -> torch.Tensor:

ctx.save_for_backward(scale)

return input_forward

@staticmethod

def backward(ctx, grad_backward: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:

scale, = ctx.saved_tensors

return scale * -grad_backward, None

順伝播時の挙動を forward 関数内に、誤差逆伝播時の挙動を backward 関数内にそれぞれ記述します。先述した通り、GRLはニューラルネットワークにおける誤差逆伝播時に勾配の符号を反転させる層です。基本的に必要なことはそれだけなのですが、DANNアーキテクチャ図における偏微分式を素直に実装するのであれば、勾配の符号反転と同時に行うスケーリング用の係数$\lambda$も指定できるようにしておくことが望ましいでしょう。このスケーリング係数は forward 関数の2つ目の引数として指定し、順伝播時にコンテキストオブジェクトに保存しておきます。そうしておくことで逆伝播時にコンテキストオブジェクトから参照でき、勾配のスケーリングを行うことが可能となります。 forward 関数の入力が2つとなったため、 backward 関数の戻り値も2つとなりますが、スケーリング係数に対して逆伝播させる勾配はないため None を返しておきます。

GRLの関数実装自体は以上で完了です。簡単ですね。PyTorchでの独自関数実装の入門に最適な題材かと思います。あとはお作法的な問題ではあるのですが、次に行うネットワーク実装の見通しを良くするために torch.nn.Module でラップして利用しやすくしておきます。

class GradientReversal(nn.Module):

    def __init__(self, scale: float):
        super(GradientReversal, self).__init__()
        self.scale = torch.tensor(scale)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        return GradientReversalFunction.apply(x, self.scale)

class GradientReversal(nn.Module):

def __init__(self, scale: float):

super(GradientReversal, self).__init__()

self.scale = torch.tensor(scale)

def forward(self, x: torch.Tensor) -> torch.Tensor:

return GradientReversalFunction.apply(x, self.scale)

これでPyTorchでのニューラルネットワークからGRLを利用する準備が整いました。次は実際にGRLの有無での挙動の違いを確認してみましょう。

GRLの挙動確認

ここではDANNモデルのネットワークアーキテクチャを抽象化した下記のようなシンプルなニューラルネットワークを考えます。

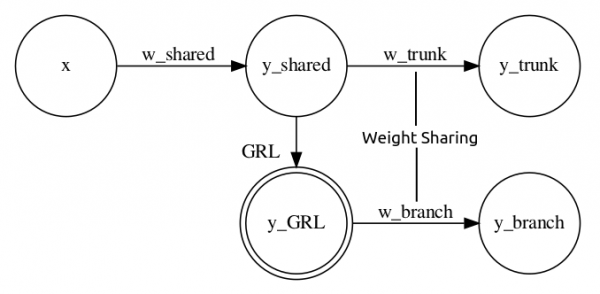
BranchReversalSiameseNet

入力として任意のベクトルを受け取り共通層を経たあとTrunk層とBranch層へと分岐するのですが、Branch層のみ直前にGRLを配置することでBranch側から逆伝搬された勾配のみ符号反転を行うアーキテクチャです。また、GRLの有無に伴う逆伝播の確認を簡単にするため、Trunk層とBranch層における出力値への影響が等しくなるように両者間での重みを共有するSiamese構造にしています。GRL以外の隠れ層は入力・出力テンソルの次元が全て1次元でバイアス項なしの全結合層とし、GRLのスケーリング係数は1.0を設定しておきます。GRLが正しく機能していれば、Trunk側から逆伝搬されてくる勾配が相殺され、共通層に届く勾配値が0となるはずです。

このアーキテクチャの実装コードは下記になります。

class BranchReversalSiameseNet(nn.Module):

    def __init__(self, use_grl: bool = True):
        super(BranchReversalSiameseNet, self).__init__()
        self.use_grl = use_grl
        self.shared = nn.Linear(1, 1, bias=False)
        self.trunk_branch = nn.Linear(1, 1, bias=False)
        self.grl = GradientReversal(scale=1.0)

    def forward(self, x: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        y_shared = self.shared(x)
        y_trunk = self.trunk_branch(y_shared)
        if self.use_grl:
            y_shared = self.grl(y_shared)
        y_branch = self.trunk_branch(y_shared)
        return y_trunk, y_branch

class BranchReversalSiameseNet(nn.Module):

def __init__(self, use_grl: bool = True):

super(BranchReversalSiameseNet, self).__init__()

self.use_grl = use_grl

self.shared = nn.Linear(1, 1, bias=False)

self.trunk_branch = nn.Linear(1, 1, bias=False)

self.grl = GradientReversal(scale=1.0)

def forward(self, x: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:

y_shared = self.shared(x)

y_trunk = self.trunk_branch(y_shared)

if self.use_grl:

y_shared = self.grl(y_shared)

y_branch = self.trunk_branch(y_shared)

return y_trunk, y_branch

それではGRLの有無による誤差逆伝播を実際に確かめて行きたいと思います。上記クラスをインスタンス化し、ランダム値を入力してTrunk層とBranch層からの出力を合算した値から誤差逆伝播を行い、共通層へ届いた勾配情報を表示するようなスクリプトを記述してみました。最初にネットワーク初期化時の各層の重みも確認のために表示しています。

print('===== BranchReversalSiameseNet Parameters ======')
torch.manual_seed(0)
model = BranchReversalSiameseNet()
print(f'Shared Weight: {list(model.shared.parameters())[0].data}')
print(f'Trunk/Branch Weight: {list(model.trunk_branch.parameters())[0].data}')
print()

print('===== BranchReversalSiameseNet w/o GRL =========')
torch.manual_seed(0)
model = BranchReversalSiameseNet(use_grl=False)
x = torch.randn(1)
print(f'Input: x={x.data}')
y_trunk, y_branch = model(x)
y_out = y_trunk + y_branch
print(f'Output: y_trunk={y_trunk.data}, y_branch={y_branch.data}, y_out={y_out.data}')
y_out.backward()
print(f'Shared Gradient: {list(model.shared.parameters())[0].grad}')
print()

print('===== BranchReversalSiameseNet w/ GRL =========')
torch.manual_seed(0)
model = BranchReversalSiameseNet()
x = torch.randn(1)
print(f'Input: x={x.data}')
y_trunk, y_branch = model(x)
y_out = y_trunk + y_branch
print(f'Output: y_trunk={y_trunk.data}, y_branch={y_branch.data}, y_out={y_out.data}')
y_out.backward()
print(f'Shared Gradient: {list(model.shared.parameters())[0].grad}')
print()

print('===== BranchReversalSiameseNet Parameters ======')

torch.manual_seed(0)

model = BranchReversalSiameseNet()

print(f'Shared Weight: {list(model.shared.parameters())[0].data}')

print(f'Trunk/Branch Weight: {list(model.trunk_branch.parameters())[0].data}')

print()

print('===== BranchReversalSiameseNet w/o GRL =========')

torch.manual_seed(0)

model = BranchReversalSiameseNet(use_grl=False)

x = torch.randn(1)

print(f'Input: x={x.data}')

y_trunk, y_branch = model(x)

y_out = y_trunk + y_branch

print(f'Output: y_trunk={y_trunk.data}, y_branch={y_branch.data}, y_out={y_out.data}')

y_out.backward()

print(f'Shared Gradient: {list(model.shared.parameters())[0].grad}')

print()

print('===== BranchReversalSiameseNet w/ GRL =========')

torch.manual_seed(0)

model = BranchReversalSiameseNet()

x = torch.randn(1)

print(f'Input: x={x.data}')

y_trunk, y_branch = model(x)

y_out = y_trunk + y_branch

print(f'Output: y_trunk={y_trunk.data}, y_branch={y_branch.data}, y_out={y_out.data}')

y_out.backward()

print(f'Shared Gradient: {list(model.shared.parameters())[0].grad}')

print()

自分の環境において、上記スクリプトの実行結果は下記になりました。いずれも順伝播時の出力自体は等しいものの、GRLありの場合は誤差逆伝播後に共通層へ伝搬されてきた値は0になっており、GRLを利用していない場合とで違いが現れたことが確認できました。

===== BranchReversalSiameseNet Parameters ======
Shared Weight: tensor([[-0.0075]])
Trunk/Branch Weight: tensor([[0.5364]])

===== BranchReversalSiameseNet w/o GRL =========
Input: x=tensor([-0.2905])
Output: y_trunk=tensor([0.0012]), y_branch=tensor([0.0012]), y_out=tensor([0.0023])
Shared Gradient: tensor([[-0.3117]])

===== BranchReversalSiameseNet w/ GRL ==========
Input: x=tensor([-0.2905])
Output: y_trunk=tensor([0.0012]), y_branch=tensor([0.0012]), y_out=tensor([0.0023])
Shared Gradient: tensor([[0.]])

===== BranchReversalSiameseNet Parameters ======

Shared Weight: tensor([[-0.0075]])

Trunk/Branch Weight: tensor([[0.5364]])

===== BranchReversalSiameseNet w/o GRL =========

Input: x=tensor([-0.2905])

Output: y_trunk=tensor([0.0012]), y_branch=tensor([0.0012]), y_out=tensor([0.0023])

Shared Gradient: tensor([[-0.3117]])

===== BranchReversalSiameseNet w/ GRL ==========

Input: x=tensor([-0.2905])

Output: y_trunk=tensor([0.0012]), y_branch=tensor([0.0012]), y_out=tensor([0.0023])

Shared Gradient: tensor([[0.]])

共通層に逆伝播されてくる勾配の値を手計算でも求めてみたいと思います。出力$y_{\mathrm{out}}$に対する共通層の重み$w_{\mathrm{shared}}$での偏微分$\frac{\partial y_{\mathrm{out}}}{\partial w_{\mathrm{shared}}}$を連鎖律を使って展開し、実行時に表示されていた入力値と各層の重みを代入してみましょう。

GRLなし

$$
\begin{eqnarray}
\frac{\partial y_{\mathrm{out}}}{\partial w_{\mathrm{shared}}}
&=& \frac{\partial y_{\mathrm{out}}}{\partial y_{\mathrm{trunk}}} \cdot \frac{\partial y_{\mathrm{trunk}}}{\partial w_{\mathrm{shared}}}
+ \frac{\partial y_{\mathrm{out}}}{\partial y_{\mathrm{branch}}} \cdot \frac{\partial y_{\mathrm{branch}}}{\partial w_{\mathrm{shared}}}\nonumber \\
&=& \frac{\partial y_{\mathrm{out}}}{\partial y_{\mathrm{trunk}}} \cdot \frac{\partial y_{\mathrm{trunk}}}{\partial y_{\mathrm{shared}}} \cdot \frac{\partial y_{\mathrm{shared}}}{\partial w_{\mathrm{shared}}}
+ \frac{\partial y_{\mathrm{out}}}{\partial y_{\mathrm{branch}}} \cdot \frac{\partial y_{\mathrm{branch}}}{\partial y_{\mathrm{shared}}} \cdot \frac{\partial y_{\mathrm{shared}}}{\partial w_{\mathrm{shared}}}\nonumber \\
&=& 1 \cdot w_{\mathrm{trunk}} \cdot x + 1 \cdot w_{\mathrm{branch}} \cdot x\nonumber \\
&=& 0.5364 \cdot (-0.2905) + 0.5364 \cdot (-0.2905)\nonumber \\
&=& -0.3116
\end{eqnarray}
$$

GRLあり

$$
\begin{eqnarray}
\frac{\partial y_{\mathrm{out}}}{\partial w_{\mathrm{shared}}}
&=& \frac{\partial y_{\mathrm{out}}}{\partial y_{\mathrm{trunk}}} \cdot \frac{\partial y_{\mathrm{trunk}}}{\partial w_{\mathrm{shared}}}
+ \frac{\partial y_{\mathrm{out}}}{\partial y_{\mathrm{branch}}} \cdot \frac{\partial y_{\mathrm{branch}}}{\partial w_{\mathrm{shared}}}\nonumber \\
&=& \frac{\partial y_{\mathrm{out}}}{\partial y_{\mathrm{trunk}}} \cdot \frac{\partial y_{\mathrm{trunk}}}{\partial y_{\mathrm{shared}}} \cdot \frac{\partial y_{\mathrm{shared}}}{\partial w_{\mathrm{shared}}}
+ \frac{\partial y_{\mathrm{out}}}{\partial y_{\mathrm{branch}}} \cdot \frac{\partial y_{\mathrm{branch}}}{\partial y_{\mathrm{GRL}}} \cdot \frac{\partial y_{\mathrm{GRL}}}{\partial y_{\mathrm{shared}}} \cdot \frac{\partial y_{\mathrm{shared}}}{\partial w_{\mathrm{shared}}}\nonumber \\
&=& 1 \cdot w_{\mathrm{trunk}} \cdot x + 1 \cdot w_{\mathrm{branch}} \cdot (-\lambda) \cdot x\nonumber \\
&=& 0.5364 \cdot (-0.2905) + 0.5364 \cdot (-1) \cdot (-0.2905)\nonumber \\
&=& 0
\end{eqnarray}
$$

ちゃんとコード実行時に表示された勾配値が得られました。GRLありの途中式2項目、Branch側の逆伝播に含まれている符号反転スケーリング係数$-\lambda$がポイントですね。

おわりに

本記事ではPyTorchでGRLの実装を行い、実際にモデルに組み込んで誤差逆伝播時の挙動を確認しました。これで無事DANNの実装へ進むことができそうで一安心です。今回のコードの全体については下記のGistにまとめてありますので、よろしければこちらもご参照ください。

https://gist.github.com/ciela/2656510f15d2a1e7c5cef206f8328cb2

ちなみに今回の件はサイバーエージェントAI事業本部にて本業の20%の時間を自分の好きな研究活動に費やすことができるゼミ制度での取り組みに端を発するものです。半期ごとに成果目標を掲げて活動計画を提出することで運営から予算を取得し、本業ではなかなか触れることの出来ないデータやモデル検証に挑戦する時間を業務中に得ることが出来る貴重な制度となっています。

Author

Kazuhiro