AutoMLチームの野村です．
本稿では，Information Geometric Optimization (IGO) という確率的最適化の枠組みと，そのIGOに対してImportance Samplingによるサンプルの再利用を導入した論文[1]について解説を行います．
Information Geometric Optimization (IGO) [2] はBlack-box最適化のためのフレームワークであり，CMA-ES(の更新式の一部)やEstimation of Distribution Algorithmなどの優れた進化計算手法の一般化にもなっています．
IGOを知ると，これらの進化計算手法というのは確率的勾配降下法の一種であるという見方ができるようになります．

IGO

IGOでは，もともとの変数空間自体を最適化する代わりに，その変数空間に探索点を生成する確率分布のパラメータを最適化します．これにより，通常のBlack-box最適化では勾配が利用できないのに対し，確率分布のパラメータ空間で議論をすることにより，勾配を計算することが可能になります．IGO自体は連続の定義域に限らず扱える枠組みですが，本稿では分かりやすさのために連続変数の最適化を仮定して話を進めるのでご注意ください（具体的には，目的関数のレベルセットのルベーグ測度が\(0\)であるという，連続最適化では自然な仮定を置きます）．

IGOでは，自然勾配を利用して探索を進めます．自然勾配とは，固定された微小なKL divergenceのもとで，最も目的関数値が減少する方向のことです．確率分布のパラメータ空間における自然勾配は，通常の行列に対して，フィッシャー情報行列の逆行列を掛けることで導出されます．自然勾配法の詳細については，例えば文献[3]をご覧ください．嬉しいことに，多変量正規分布やベルヌイ分布をはじめとするいくつかの確率分布については，自然勾配が解析的に導出されているので，これらの確率分布をIGOのモデルに用いる場合には，フィッシャー情報行列をデータから推定する必要はなくなります．これは，ディープラーニングの重みパラメータ最適化のために自然勾配法が用いられる状況とは異なるものだと思います．

それではフォーマルな定式化を行います．我々のゴールは目的関数\(f : \mathbb{X} \mapsto \mathbb{R}\)の最小化です．IGOでは，この\(f\)を最小化する\(x^{\ast} \in \mathbb{X}\)を探そうとする代わりに，以下の式，
$$\begin{align}
J_{\theta^{(t)}}(\theta) = \int W_{\theta^{(t)}}^{f} (x) p_{\theta}(x) dx
\end{align}$$
を最大にする\(\theta^{\ast} \in \Theta\)を探します．ここで注目していただきたいのは，\(f\)の代わりにutility関数\(W_{\theta^{(t)}}^{f}\)が使われている点です．なぜ\(f\)を使わずに，\(W_{\theta^{(t)}}^{f}\)を使うのでしょうか？

\(f\)を使った場合には素直な確率緩和が可能になる一方で，目的関数に対する単調変換に対して不変ではありません．これは実用上，ロバストでないという点で望ましくないと言えそうです．そこで，IGOでは，目的関数の単調変換に対して不変となるよう，\(f\)の代わりに\(W_{\theta^{(t)}}^{f}\)を用いています．ここで\(W_{\theta^{(t)}}^{f}\)は，
$$\begin{align}
q^{\leq}_{\theta^{(t)}}(x) = P_{\theta^{(t)}}[y : f(y) \leq f(x)]
\end{align}$$
で定義される\(f(x)\)の分位点と，単調比増加関数\(w : [0, 1] \mapsto \mathbb{R}\)を用いて，
$$\begin{align}
W_{\theta^{(t)}}^{f}(x) = w(q^{\leq}_{\theta^{(t)}}(x))
\end{align}$$
で定義されます（定義域が連続以外の場合にはもう少し複雑になります）．

あとは，上記によって定義した\(J_{\theta^{(t)}}(\theta)\)を自然勾配法により更新します．
単純な式変形により，
$$\begin{align}
\nabla J_{\theta^{(t)}}(\theta) &= \nabla \int W_{\theta^{(t)}}^{f} (x) p_{\theta}(x) dx \\
&= \mathbb{E}_{x \sim p_{\theta}(x)} [W_{\theta^{(t)}}^{f} (x) \ln \nabla p_{\theta}(x)]
\end{align}$$
が得られるので，これにフィッシャー情報行列の逆行列を掛けることで自然勾配が求まります．

全体のアルゴリズムの流れは以下になります．

• \(\lambda\)個の解\(x_1, \cdots, x_{\lambda}\)を，\(P_{\theta}\)からサンプル
•  それぞれの解を評価する
•  解とその評価値を使って，自然勾配を計算し，確率分布のパラメータ\(\theta\)を更新

実用上は有限の\(\lambda\)を用いるため，以下の2点において有限サンプルでの近似が必要です．

• \(\nabla J_{\theta^{(t)}}(\theta) = \mathbb{E}_{x \sim p_{\theta}(x)} [W_{\theta^{(t)}}^{f} (x) \ln \nabla p_{\theta}(x)]\)
• \(q^{\leq}_{\theta^{(t)}}(x) = P_{\theta^{(t)}}[y : f(y) \leq f(x)]\)

まず\(\nabla J_{\theta^{(t)}}(\theta)\)については，モンテカルロ法により期待値を推定します．
$$\begin{align}
\nabla J_{\theta^{(t)}}(\theta) \approx \frac{1}{\lambda} \sum_{i=1}^{\lambda} W_{\theta^{(t)}}^{f} (x_i) \ln \nabla p_{\theta}(x_i).
\end{align}$$
同様に，\(q^{\leq}_{\theta^{(t)}}(x)\)も以下で推定を行います．
$$\begin{align}
q^{\leq}_{\theta^{(t)}}(x) \approx \frac{1}{\lambda} {\rm rk}^{\leq}(x_i) := \frac{1}{\lambda} \sum_{k=1}^{\lambda} \mathbb{I}\{ f(x_k) \leq f(x_i) \}.
\end{align}$$

サンプルの再利用

それでは，上記の推定精度のあげるための，Importance Samplingを用いたサンプルの再利用について説明します．
いま，\(K + 1\)個の確率分布\(p^{k} \ (k = 0, \cdots, K)\)とそれぞれの確率分布からのサンプルに対応する\(x_i^k (i = 1, \cdots, \lambda)\)が存在するとします．ここで，\(k\)は現在の世代を0として，どれだけ古い世代まで遡るかのインデックスを表しているものとします．ここでの目的を期待値\(\int g(x) p^{0}(x) dx\)を推定することだとすると，一番ナイーブな方法は\(p^{0}\)からの解のみを使って，\(\sum_{i=1}^{\lambda} g(x_i^{0}) / \lambda\)と計算することだと思います．

しかしこの方法では，\(x_i^k (k \geq 1)\)のサンプルを全て捨ててしまっており，情報を有効活用できていないという問題が考えられます．そこで，上記の代わりに，\(\bar{p}(x) = (K+1)^{-1} \sum_{k=0}^K p^k (x)\)として以下の推定量を用いることにします．
$$\begin{align}
\frac{1}{\lambda (K + 1)} \sum_{k=0}^{K} \sum_{i=1}^{\lambda} g(x_i^k) \frac{p^0 (x_i^k)}{\bar{p} (x_i^k)}
\end{align}$$
これはunbiasedであり，かつ，naiveなImportance Sampling (つまり，提案分布に\(p_k\)を用いたもの)より分散が小さくなります．こちらの推定量を，論文では\(q^{\leq}_{\theta^{(t)}}(x)\)と\(\nabla J_{\theta^{(t)}}(\theta)\)の推定に用いています．

実験と結果
上記の方法を実装したCMA-ES[4]について，20次元ベンチマーク関数に対する実験の結果を以下に示します（CMA-ESについてご存知ない方は，こちらの記事が挙動を理解する上で参考になります）．

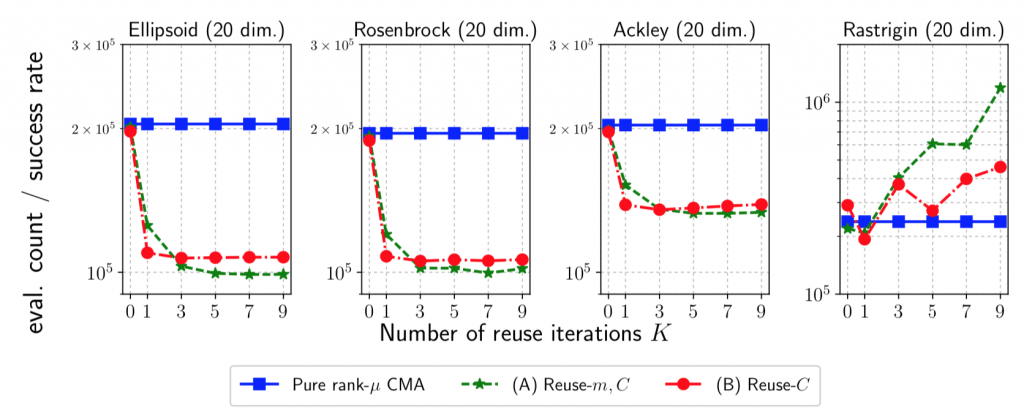
青線が元々のCMA-ES，緑線が平均ベクトルと共分散行列の更新にサンプルの再利用を適用したもの，赤線が共分散行列の更新のみにサンプルの再利用を適用したものになっています．また，横軸がどのくらい前の世代までのサンプルを用いるかという\(K\)の値，縦軸は最適解への収束までに必要だった評価回数 / 成功率になります（つまり，低いほど良いと言えます）．左３つの結果では，サンプルの再利用によって大幅に性能改善ができています（論文内では，Sphere関数などの他のベンチマーク関数でも同様の結果が見られたことが述べられています）．
一方で，右のRastrigin関数では，\(K\)の値を大きくするにつれて性能が悪化しています．Rastrigin関数は強い多峰性を有する関数であり，局所解に収束してしまったことを示唆しています．現在のサンプルと過去のサンプルとの間に存在する相関を無視して，独立として扱った上でImportance Samplingをしていますが，こちらが原因かもしれないという考察がなされています．

最後に
本稿では，IGOにサンプルの再利用の工夫を導入することで性能改善を行った論文を紹介しました．IGOは様々な手法の一般化となっているので，IGOに対する改善はこれら多くの手法に対して同時に改善を行えるため価値が高いと感じました．本稿ではPBILの実験や実験の考察を含めた様々な点を省略しているので，もし気になった点がある方は元論文の方を見ていただけると幸いです．最後までお読みいただき，ありがとうございました．

References

[1] Shinichi Shirakawa, Youhei Akimoto, Kazuki Ouchi, and Kouzou Ohara. Sample reuse via importance sampling in information geometric optimization. arXiv preprint arXiv:1805.12388, 2018.

[2] Yann Ollivier, Ludovic Arnold, Anne Auger, and Nikolaus Hansen. Information-geometric optimization algorithms: A unifying picture via invariance principles. The Journal of Machine Learning Research, 18(1):564–628, 2017.

[3] Shun-Ichi Amari. Natural gradient works efficiently in learning. Neural computation, 10(2):251–276, 1998.

[4] Nikolaus Hansen. The CMA Evolution Strategy: A tutorial. arXiv preprint arXiv:1604.00772, 2016.