AI Lab Algorithmsチームの野村です．今回は離散変数と連続変数の両方を含むようなブラックボックス最適化に対する手法を提案した研究について概説します．この研究成果は進化計算分野におけるトップカンファレンスであるGECCO2023に採択されています．論文はこちらです．

ブラックボックス最適化とは？

産業や科学などの多くの領域で，具体的な式が得られていない関数に対して最小値 (あるいは最大値) を探索したい場合があります．例えば機械学習アルゴリズムのハイパーパラメータ最適化では，より良い汎化誤差を達成する機械学習モデルを獲得するために，良い検証誤差を達成するハイパーパラメータを探索します．この問題では，ハイパーパラメータに依存する形で検証誤差を直接計算する数式は一般には得ることができません．このような場合に，入力 (ハイパーパラメータ) と出力 (検証誤差) の関係のみを用いる，つまり，評価値が計算される過程を‘‘ブラックボックス’’と見做して最適化を行う枠組みをブラックボックス最適化といいます．

既存手法: CMA-ES with Margin と (1+1)-CMA-ES

CMA-ES: ブラックボックス最適化に対する有力な手法の1つとして，確率的な最適化アルゴリズムの一種であるCMA-ESがあります．CMA-ESは多変量正規分布からの解の生成により有望な解を探索します．このとき，より有望な領域へ解を生成できるように，正規分布のパラメータである平均ベクトルと共分散行列を逐次的に更新していきます．通常，CMA-ESは連続変数のみを対象に実行されます．

CMA-ES with Margin: CMA-ES with Marginは，整数などの離散的な変数を含む最適化に対して適用できるようにCMA-ESを拡張した手法であり，混合整数ブラックボックス最適化に対するstate-of-the-artな手法の1つです．連続変数を単純に離散化した上で従来のCMA-ESを適用する方法では，離散変数に対応する次元の正規分布の分散が小さくなってしまうことで，特定の領域のみに解を生成するようになり探索に失敗することがあります．CMA-ES with Marginでは正規分布のパラメータを適切に補正することでそれらの問題に対処しています．分布パラメータの補正操作の詳細については，論文に加えて，論文の筆頭著者である濱野さんが公開されているこちらのスライド等をご参照ください．CMA-ES with Marginはブラックボックス最適化/ハイパーパラメータ最適化の著名なOSSであるOptunaにも導入されています．

(1+1)-CMA-ES: 本研究では，CMA-ESの変形の一種である(1+1)-CMA-ESという手法を活用します．(1+1)-CMA-ESは，常に最良解を平均ベクトルに設定するという「エリート性」を特徴に持つ方法です．単峰性関数などの比較的簡単な構造を有する問題に対して，(1+1)-CMA-ESは通常のCMA-ESと比較して良好な性能を示すことが報告されています．一方で，(1+1)-CMA-ESもCMA-ESと同様に連続変数を対象にした手法であり，離散変数を含む問題に対する拡張は行われていませんでした．

提案手法: (1+1)-CMA-ES with Margin

本研究では(1+1)-CMA-ESについて，効率性を保ちつつ，離散変数と連続変数の両方を含むような問題に対して適用できるように拡張を行いました．この拡張はCMA-ES with Marginにおいて導入された補正操作を基にして行われますが，CMA-ES with Marginにおける補正は通常のCMA-ESに対して導入されたものであったため，本研究では(1+1)-CMA-ESに適合するようにこの補正操作を改良しています．

既存手法CMA-ES with Marginと提案手法(1+1)-CMA-ES with Marginについて，実問題で重要となる性質を有するベンチマーク問題において実験を行った結果を以下の図に示しています．縦軸は最適解発見までに必要だった評価回数を成功率で割ったものであり，低ければ低いほど良い収束性能であることを意味します．横軸はベンチマーク問題の次元数です．提案手法はこれら全てのベンチマーク問題において既存手法であるCMA-ES with Marginよりも高速な収束を達成しています．

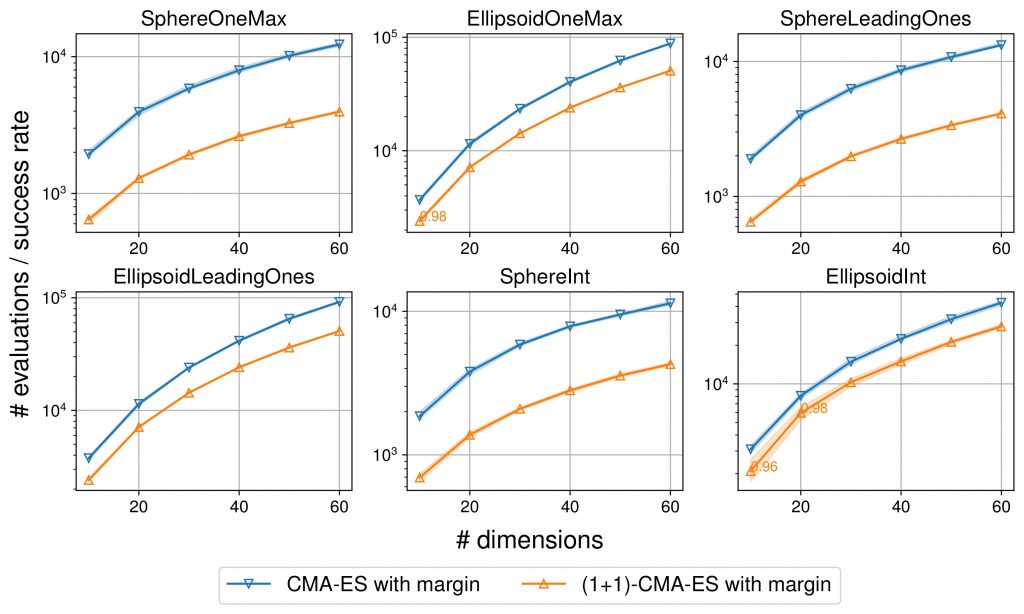
既存手法CMA-ES with Marginと提案手法(1+1)-CMA-ES with Marginの比較．縦軸は最適解発見までに必要だった評価回数を成功率で割ったものであり，低いほど良い．横軸は最適化問題の次元数．

まとめ

本研究では，離散変数と連続変数の両方を含むようなブラックボックス最適化のための有力な手法として(1+1)-CMA-ES with Marginを提案しました．連続変数用の有力手法である(1+1)-CMA-ESについて，効率性を保った上で，離散的な変数を含む問題に対して適用できるよう拡張を行いました．Python実装も公開されているので，気になった方はぜひ使ってみていただけると幸いです．