Blog
【採択論文紹介】CMA-ES for Discrete and Mixed-Variable Optimization on Sets of Points (PPSN2024)
AI Lab Algorithmsチームの濱野です.本稿では,座標点集合からの選択を変数に含むブラックボックス最適化問題に適用可能な手法を提案した研究について解説します.本研究成果は,進化計算分野におけるトップカンファレンスであるPPSN2024に採択されています.
Kento Uchida, Ryoki Hamano, Masahiro Nomura, Shota Saito, and Shinichi Shirakawa. CMA-ES for Discrete and Mixed-Variable Optimization on Sets of Points. In Proceedings of the 18th International Conference on Parallel Problem Solving from Nature (PPSN’24), 2024. [arXiv]
本研究が対象とする問題
最適化問題とは,ある目的関数を最小化あるいは最大化するような変数を発見する問題のことを指します.目的関数が明示的に与えられている場合は,目的関数の微分情報などを用いて最適化を行うことができます.一方で,産業や科学の領域では目的関数が明示的に与えられないケースが存在し,そのような最適化問題はブラックボックス最適化問題と呼ばれています.ブラックボックス最適化問題では,入力となる変数とそれに対応する目的関数値の関係のみを用いて最適化を行うことになります.
本研究では「座標集合からの選択」を変数として含むブラックボックス最適化を考えます.例として風車の設置計画問題 [1]を考えてみます.この問題では,発電量が最大となるような「風車の形状」「風車の設置位置」を探索するとします.さらに「風車の形状」は連続変数で決定されるのに対し,「風車の設置位置」は設置可能な座標の候補から1つを選択することで決定されるとします.
「候補から1つを選択する」ということから,「風車の設置位置」はカテゴリ変数として扱うのが自然かもしれません.しかしカテゴリ変数として扱ってしまうと,設置位置の位置関係を利用することができません.例えば,近い設置位置への変更よりも,遠い設置位置への変更の方が目的関数への影響が大きいと予想できます.そのため,設置位置の位置関係を考慮することで効率的に最適化することのできる手法が望まれています.
提案手法
本研究では,「座標集合からの選択」を変数として含むブラックボックス最適化問題に適用可能なCMA-ES on sets of points (CMA-ES-SoP)を提案しました.CMA-ES-SoPは連続最適化を行う進化計算法であるCovariance Matrix Adaptation Evolution Strategy (CMA-ES) [2]をベースにした手法であり,「座標集合からの選択」を効率的に対処可能なテクニックが導入されています.
CMA-ES-SoPでは,多変量ガウス分布から生成された連続変数を座標集合中の最近傍の点に写像することで解の候補を生成します.「連続変数がどの座標点に写像されるか」を可視化するとボロノイ図そのものになり,ボロノイ図のある領域内の連続変数は同一の点に写像されることになります.しかし,このような写像を導入しただけでは,効率的な最適化を行うことはできないことが明らかになっています.
図1に,座標集合とそれに対するボロノイ図,多変量ガウス分布を可視化したものを表示しています.多変量ガウス分布がボロノイ図の1つの領域内に収束してしまうと,多変量ガウス分布から生成される連続変数が全てボロノイ図の同じ領域内に存在する確率が高くなり,解の候補が1種類に固定化されてしまいます.この現象が探索の初期で起きてしまうと,最適解以外の領域に多変量ガウス分布がはまってしまう問題が起きます.そこで,ボロノイ図のある1つの領域だけでなく,その周囲の領域にも連続変数が生成されるように,多変量ガウス分布を補正することを考えます.多変量ガウス分布の平均 (中心部分) が位置している領域と隣接する領域にも連続変数が生成されるよう,多変量ガウス分布を引きのばして補正します.さらにCMA-ES-SoPでは,この補正が過剰にはたらくことを防ぐための工夫点が導入されており,固定化へのロバスト性と探索の効率性の両立が実現されています.補正方法の詳細については論文をご参照ください.
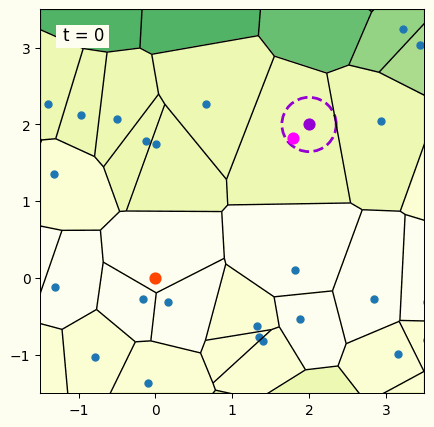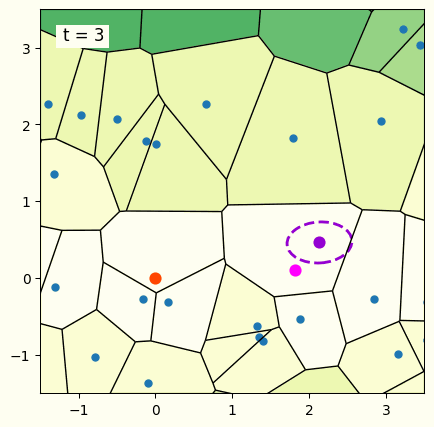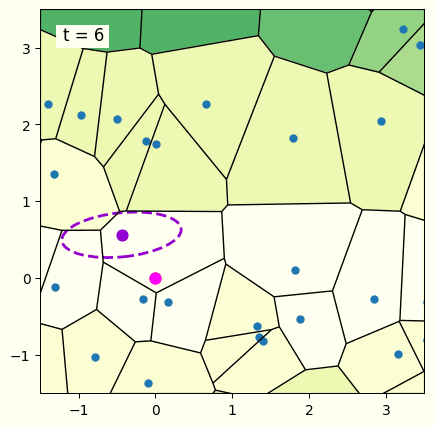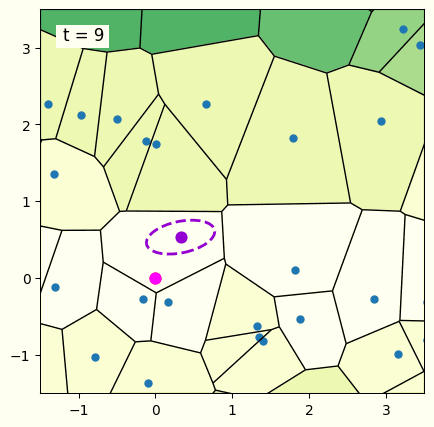
図1. CMA-ES-SoPの最適化の様子.背景の色が明るい領域ほど評価値の良い点となる.楕円の点線は解の候補を生成する多変量ガウス分布を表していて,更新を重ねるごとにオレンジ色の点で表される最適解へ近づいていることがわかる.
数値実験
実問題の最適化で重要となる性質をもつベンチマーク関数を用いて,以下の3つのバリエーションについて実験を行いました.
- CMA-ES (CMA-ES-SoPから多変量ガウス分布の補正を取り除いたもの)
- CMA-ES-SoP
- CMA-ES-SoP w/o margin adaptation (CMA-ES-SoPから「多変量ガウス分布の補正が過剰にはたらくことを防ぐための工夫点」だけを取り除いたもの)
図2に実験結果を示します.まずCMA-ESでは,分布の固定化によって評価値の改善が停滞しています.次にCMA-ES-SoP w/o margin adaptationではCMA-ESよりも評価値の改善が行われているものの,次元数が増加するにつれて評価値の改善が停滞する傾向にあります.そしてCMA-ES-SoPでは,どの設定でも効率的な最適化が行われており,分布の補正や工夫点が有効にはたらいていることが確認できました.
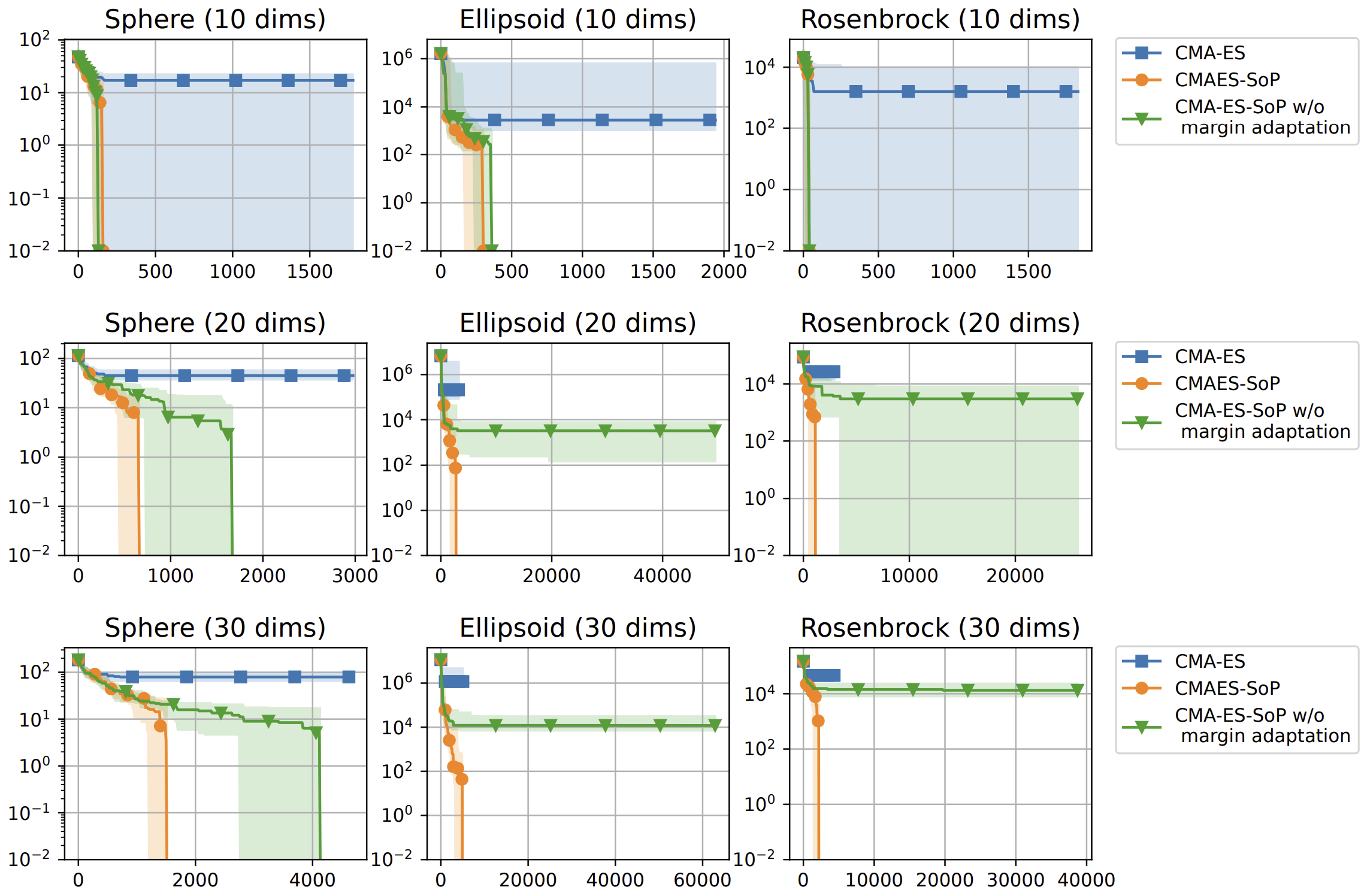
図2. 最適化中の解の最良評価値の推移.横軸は目的関数の評価回数,縦軸は最良評価値で小さいほど良い.各設定につき,25試行の中央値と四分位範囲を表示.多変量ガウス分布の分散共分散行列の最小固有値が一定値以下になるなどの終了条件を満たした場合に試行を終了している.
さいごに
本研究では座標点集合の選択を変数に含むブラックボックス最適化問題に適用可能な手法としてCMA-ES-SoPを提案しました.CMA-ES-SoPについて気になった方は,ぜひ論文を読んでいただければ幸いです.
参考文献
[1] S. Andrew Ning, Rick Damiani, and Patrick J. Moriarty. Objectives and constraints for wind turbine optimization. Journal of Solar Energy Engineering 136(4), 041010, 2014.
[2] Nikolaus Hansen. The CMA Evolution Strategy: A tutorial. arXiv preprint arXiv:1604.00772, 2016.
Author
