はじめに

GDPに代表されるマクロ指標、企業の決算といった経済の動きを表す指標は、ときに株価を変動させるほど人々の意思決定に大きな影響をもちます。他方で、経済指標は月ごと〜四半期で公表されることが多く、公表される数字も幾分古いことが多いです。データの集計や加工などに時間がかかるため、通常１ヶ月以上ラグを持って公表されます。
これらの数字をリアルタイムで推計できれば、公共政策やビジネス上非常に有用です。こうした試みをナウキャスティングと呼びます。
ナウキャスティングはすでにアトランタ連銀のGDPNowとして実用化されていますが、背景にある技術は日進月歩の状態にあります。GDPNowは月次統計をもってGDPをアップデートする試みですが、データの可用性が高まるにつれ、より高頻度のデータを用いてナウキャスティングを行う必要性が高まると考えられます。また、高頻度化とともに高次元化も進むことと思われます。具体的には、公的統計だけではなく、Googleトレンドに代表されるような検索クエリデータやSNSやニュースのテキストデータなど、多種多様なデータ（オルタナティブデータ）が予測変数として使われていくようになるでしょう。
こうして頻度と次元の両面で拡張されたデータは、しかし、教師あり学習で予測しようとすれば、自ずからデータのサイズという制約に直面します。すなわち、低頻度な経済指標は１年に４（四半期データ）〜１２（月次データ）とデータポイントが少なく、さらにオルタナティブデータは長くて１０年ほどしか遡れないため、両者を揃えるとサンプルサイズは100に満たないことになります。
このような小サンプル高頻度高次元データという環境でどのような選択肢があるのか考えてみます。

特徴量選択による手法

一般に、高次元データに対しては、LASSOによる特徴量選択が自然であると考えられます。最近公刊されたUematsu & Tanaka (2019)では、LASSO, SCAD, MCPといった特徴量選択手法をアメリカのGDP成長率の予測に用いています。これらの手法は最小二乗法に罰則項を加えるという点で共通していますが、SCADとMCPはオラクル性（Oracle Property）を持つという優位性があるとされています。オラクル性とは、サンプルサイズが無限に大きくなったときに無関係な特徴量を含んだ多数の特徴量セットから正しく関係のある特徴量を選択をできるという性質です。

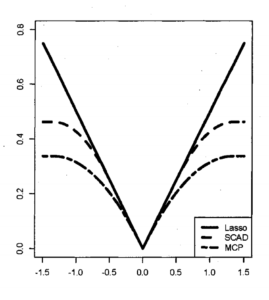
罰則項の違い。梅津 (2017)より引用

LASSO, SCAD, MCPは罰則を含んだ損失関数を最小化することにより特徴量選択と推定を同時に行う手法ですが、一旦LASSOによって特徴量選択を行ったあとに通常のOLSを行うOLS post-LASSOという手法がBelloni & Chernozhukov (2013)によって提案されています。Uematsu & Tanaka (2019)では、ベンチマークとしてOLS post-Lassoに加え、post-SCAD、post-MCPを比較手法としています。

その結果、提案手法であるLASSO/SCAD/MCPが、基本的な時系列モデルであるARモデルを含めたベンチマークに対して、ナウキャスティング及びごく近い将来の予測で高い性能を示しました。提案手法がpost-XXX手法に対して優越したのは特徴量の強い時間依存性によるものではないかと指摘しています。

MIDASモデル

低頻度な応答変数（従属変数）と高頻度な予測変数（独立変数）を整合的に取り扱う方法は、計量経済学の分野で長年検討が続けられてきました。その中で、時系列データに関するヒューリスティクスを用いて少ないパラメータで高頻度データの情報を縮約する手法としてMIDAS (Mixed DAta Sampling)モデルが提案されています（Ghysels et al., 2007）。前述したシンプルな罰則付モデルではそれぞれのラグ項について係数（重み）を推定する必要がありますが、MIDASモデルは、高頻度データを加重平均して低頻度データに変換しながら係数を推定するのでパラメータの数が少なくなります。これはデータポイントが少ない場合非常に有利です。Marsilli (2014)はMIDASにLASSOを加えたLASSO-MIDASモデルを提案しています。これは単純に、MIDASモデルにLASSO項をつけたものです。さらに、Marsilliと同じフランス銀行のMogliani (2019)は、MIDASモデルに、Adaptive Group LASSOという特徴量選択手法とSpike and Slabというベイズ統計における特徴量選択を組み合わせた手法を提案しています。Uematsu & Tanaka (2019)との性能比較がないので優劣はわからないものの、同様にナウキャスティングからごく近い将来の予測に関してARモデルを含んだベンチマークを凌駕しています。

次元削減

高次元データについては、特徴量選択をせずに次元削減を行うという方向性も検討されてきました。Marcellino & Schumacher (2010)はPCAやその派生型による次元削減と前述のMIDASを組み合わせたFactor-MIDASという手法を提案しています。PCAによって高次元データに対応し、MIDASを用いて高頻度データにも対応するというシンプルなアイデアで、既存のパッケージで実装できるという意味では取り掛かりやすい手法かもしれません。ちなみに、MIDASについては、Rにmidasrというパッケージが存在し、誰でも使えるようになっています。ただし、特徴量の次元がサンプルサイズを上回る場合に対応していないため、PCAで次元削減するか、一旦高頻度データを平均するなどして低頻度に変換してLASSO等で特徴量選択をしてからMIDASを適応すると行った工夫が必要となります。

おわりに

今回は、高次元、高頻度、小サンプルデータにおいて用いられる手法を最近の論文にもとづいて簡単に解説しました。MIDAS以外にも状態空間モデルを用いる手法が考えられますが、最初に適応する手法としては以上のような手法がよいのではないでしょうか。

引用文献

Uematsu, Y., & Tanaka, S. (2019). High‐dimensional macroeconomic forecasting and variable selection via penalized regression. The Econometrics Journal, 22(1), 34-56.

Belloni, A., & Chernozhukov, V. (2013). Least squares after model selection in high-dimensional sparse models. Bernoulli, 19(2), 521-547.

梅津佑太. (2017). スパース推定における情報量規準 (量子統計モデリングのための基盤構築).数理解析研究所講究録, 第2018巻, pp.116-130

Ghysels, Eric, Arthur Sinko, and Rossen Valkanov. “MIDAS regressions: Further results and new directions.” Econometric Reviews 26.1 (2007): 53-90.

Marsilli, Clément. “Variable selection in predictive midas models.” (2014).https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2531339

Mogliani, Matteo. 2019. “Bayesian MIDAS Penalized Regressions: Estimation, Selection, and Prediction.” arXiv:1903.08025 [econ]. http://arxiv.org/abs/1903.08025 (June 29, 2019).

Marcellino, M., & Schumacher, C. (2010). Factor MIDAS for nowcasting and forecasting with ragged‐edge data: A model comparison for German GDP. Oxford Bulletin of Economics and Statistics, 72(4), 518-550.