Blog
ミニ花札のAIを作ってみよう
AI Labの阿部 (@bakanaouji) です.
今年の7月に,6人プレイヤのポーカーのAIであるPluribus[1]が発表され,多人数不完全情報ゲームが着々と攻略されつつあるということを印象づけました.
今回は,不完全情報ゲームで戦略を計算するために使われるアルゴリズムであるCounterfactual Regret Minimization (CFR) [2]を花札「こいこい」に適用することで,このゲームにおけるAIを作成してみたいと思います.
Counterfactual Regret Minimization
CFRは,ナッシュ均衡戦略を効率的に計算するためのアルゴリズムで,二人零和不完全情報ゲームにおいてナッシュ均衡戦略を計算できることが保証されています.1
CFRは複数回のiterationを繰り返すアルゴリズムで,各iterationごとに「この行動を取ったほうが良かった」という後悔 (counterfactual regret) を元にして戦略を更新します.ここで,counterfactual regretは,「現在の戦略\(\sigma^t\)を情報集合\(I\)2で行動\(a\)を取るように変更したら,自分 (プレイヤ \(i\)) の利得\(u_i\)がどの程度増加するのか」を表している指標であり,以下の式で定義されます3.
$$
r_i^t(I,a)=\pi_{-i}^{\sigma^t}(I)(u_i(\sigma^t_{I\to a},I)-u_i(\sigma^t,I))
$$
各iteration \(t\)ごとの戦略更新アルゴリズムをざっくりとまとめると,以下のようになります.
- 情報集合\(I\)に対して,以下の2つの価値を計算
- 現在の戦略\(\sigma^t\)の期待利得 : \(u_i(\sigma^t, I)\)
- \(I\)で行動\(a\)を取るように変更した戦略の期待利得 : \(u_i(\sigma_{I\to a}^t,I)\)
- \(u_i(\sigma^t, I)\),\(u_i(\sigma_{I\to a}^t,I)\)を元にregret \(r_i^t(I,a)\)を計算
- \(r_i^t(I,a)\)を元に,戦略を更新4
$$\sigma_i^{T+1}(I,a)=
\frac{\max(R_i^T(I,a),0)}{\sum_{a\in A(I)} \max(R_i^T(I,a),0)}
$$
ただし,\(R_i^T(I,a)=\sum_{t=1}^T r_i^t(I,a)\)であり,\(A(I)\)は\(I\)で取ることができる行動の集合を意味しています. - ゲーム木をルートノードから順にたどっていき,各情報集合\(I\)に対してstep 1からstep 3を繰り返して戦略を更新.
CFRは,ゲームの情報集合数が\(O(10^{12})\)程度であれば現実的な時間でナッシュ均衡戦略を計算できることが知られています.
花札「こいこい」
花札は日本で古くから親しまれてきたカードゲームで,一組48枚 (12ヶ月×4枚) の札を用いてプレイします.花札には様々な遊び方を存在しますが,最も馴染みが深いのは映画でも登場したことがある「こいこい」ではないでしょうか.
こいこいでは,以下のような流れでゲームを行います.
1. 各プレイヤに8枚ずつ手札を配り,場に8枚の札を表向きに配る.残りの札は山札として裏向けに積む.
2. 親プレイヤから順番に手札から好きな札を一枚場に出す.場札に同じ「月」の札があれば,自分が出した札と,同じ「月」の札,両方を合札 (自分の持ち札) に加える.なければ,自分が出した札を場札に加える.
3. 山札から1枚札をめくり,同様に同じ月の札があれば合札とし,なければ場札に加える.
4. 合札の中に指定の札の組み合わせを満たす「役」が成立していた場合,「あがり」か「こいこい」かを選択する.「あがり」の場合,プレイヤは役に応じた得点をもらいゲームを終了する.「こいこい」の場合,ゲームを終了せずに続行する.
5. step 2からstep 4をゲーム終了まで繰り返す.なお,両方のプレイヤの手札がなくなった場合にはどちらのプレイヤにも得点を与えずにゲームを終了する.
ゲームの名前にもなっていることからわかるように,「こいこい」するかどうかを決定することが,このゲームの最も特徴的な要素となっています.より高い得点が得られそうだからゲームを続行したいこともあるけれど,欲張って「こいこい」すると逆に相手にあがられて得点が台無しになってしまうこともあるため,絶妙な駆け引きが必要になります.
ミニ花札
「こいこい」における初期の手札,場札の組み合わせ数を考えてみると,それだけで情報集合数が\(10^{16}(< {}_{48}C_8\times {}_{40}C_8)\)を超えてしまいます.情報集合数が大きすぎるため,CFRによって現実的な実行時間で戦略を計算することは難しそうです.5
この問題に対処するために,ポーカーでは抽象化した小さなゲームを考えることによって情報集合数を削減する,Abstractionというテクニックがよく使われます.今回は,Abstractionとは少し異なりますが,使う札の数や手札・場札数を少なくしたミニバージョンの花札を考え,そのゲームでの均衡戦略をCFRによって計算したいと思います.
ミニ花札では,以下の9枚 (3ヶ月×3枚) の札のみを用いるようにします.

また,最初に配る手札の枚数は2枚ずつ,場札は1枚のみとかなり限定してしまいます.使用する札を限定している分,役も成立しにくくなってしまうため,ほとんどのケースで両方のプレイヤが得点を得られずにゲームが終了してしまう可能性があります.そこで,「こいこい」でよく用いられる役の成立条件を少し緩めたり,新しい役を追加することで,役が成立しやすいゲームへと仕立て上げます.
具体的には,以下のような役を用いました.
- 二光 (3点)

- 花見で一杯 (5点)

- 月見で一杯 (5点)

- タネ (1点)

- タン (1点)

- カス (1点)

かなり簡略化をしたため,各プレイヤが意思決定を行う回数が2,3回程度とかなり少なくなってしまったものの,依然としてこいこい判断などの特徴的な要素は残っているため,フルサイズの花札の戦略を検討するファーストステップとしては良いかもしれません.ただし,最初に配られる場札が1枚で手札が2枚なので,親プレイヤはどのようなプレイをしてもこいこいをする機会がないということは注意が必要です.
実験 : ミニ花札へのCFRの適用
では実際にミニサイズの花札にCFRを適用し,それによって得た戦略がどの程度強いものであるのか評価してみましょう.
CFRのアルゴリズムはchance samplingというテクニックを用いたversionのものを使用しました.今回の実験ではCFRの総iteration数は500万iterationとしました.また,「片方のプレイヤの得た得点にマイナス1をかけた値をもう一方のプレイヤの利得とする」ことで,利得が零和になるように扱いました.
ランダムプレイヤとの対戦
まず,CFRによって得た戦略を評価するために,ランダムに行動を取るプレイヤとの対戦を行いました.「こいこい」は親プレイヤが有利なゲームなので,親・子プレイヤどちらでプレイするかで期待利得に偏りが生じてしまいます.そこで,親と子を交互にプレイすることを100万回繰り返すことで,ゲームに対称性をもたせるようにしました.
各iterationごとに計算された戦略のランダムプレイヤに対する利得の平均値は以下のようになりました.
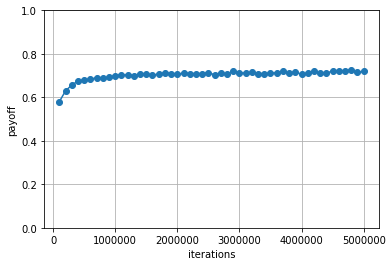
平均利得が0より大きいため,ランダムプレイヤに対しては少なくとも勝ち越すような戦略となっていることがわかります.
ルールベースプレイヤとの対戦
同様に,ルールベースで意思決定を行うプレイヤを構築し,このプレイヤとの対戦も行いました.
ルールベースプレイヤは,予め各札に点数を割り当てておき,札を取れる場合は点数の合計が最大になるように札を選択します.札を取れない場合,手札の中で点数が最低の札を出します.こいこい判断は複雑な判定が必要そうだったため,今回は「こいこいしない」で統一するようにしました.
各札に対する点数は以下のように割り当てました.

各iterationごとに計算された戦略のルールベースプレイヤに対する利得の平均値は以下のようになりました.
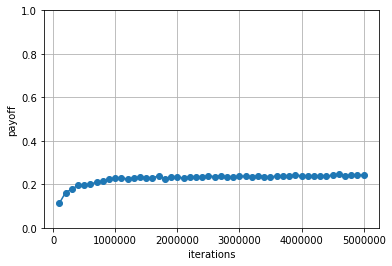
ランダムプレイヤとの対戦と比べて平均利得が低い値となっていますが,それでも0より大きい値となっているため,ルールベースプレイヤに対しても勝ち越すような戦略となっていることがわかります.
戦略の解釈
気になるのは,CFRによって得た戦略がどのような挙動をしているのか,という点です.いくつか例を挙げてみましょう.
次の状況は,CFRプレイヤが子でプレイしている状況です.このような状況では,「こいこい」する確率が0.997339となっており,ほぼ確実に「こいこい」を宣言するようでした6.

実際には,CFRプレイヤから親プレイヤの手札は見えていないことに注意が必要です.この状況からでは,こいこいしてゲームを続行したとしても親プレイヤはどんなに頑張っても”山”の札しか取得することができないため,親プレイヤに上がられる心配はありません.逆に,自分は「二光」を達成することによってさらに得点が増加する可能性もあるため,「こいこい」をしたほうが得であると判断しているようです.
次の状況は,反対に「こいこい」しない確率が0.99922と高くなった状況です.
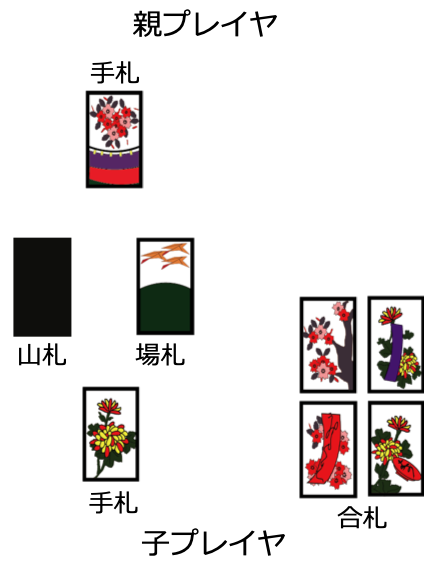
この状況では自分がさらに役を成立させるためには,「月見で一杯」もしくは「タネ」を成立させる必要がありますが,どちらも”山”の札を必要とします.しかし,この後ゲームを続行したとしても,相手がたとえ何を手札に持っていようと次の相手のターンで”山”の札は取られてしまいます.なので,「こいこい」をした場合は必ず自分の利得が0以下となってしまうため,この状況では「こいこい」しないことを選ぶようです.
おわりに
今回は,ミニサイズの花札にCFRを適用し,ナッシュ均衡戦略の近似戦略を計算しました.今回はゲームサイズをかなり小さくしたトイゲームで実験を行いましたが,今後はAbstractionなどのテクニックを用いて,フルサイズの花札のナッシュ均衡戦略を計算してみようと思っています.
最後まで読んでくださりありがとうございました.
参考文献
[1] Noam Brown and Tuomas Sandholm. Superhuman ai for multiplayer poker. Science, eaay2400, 2019.
[2] Martin Zinkevich, Michael Johanson, Michael Bowling, and Carmelo Piccione. Regret minimization in games with incomplete information. In Advances in neural information processing systems, pp. 1729–1736, 2008.
[3] Oskari Tammelin. Solving large imperfect information games using cfr+. arXiv preprint arXiv:1407.5042, 2014.
- 厳密には,ナッシュ均衡の近似戦略である\(\epsilon\)ナッシュ均衡が計算できることが保証されています. ↩
- 情報集合\(I\)とは,あるプレイヤが観測できる部分的な情報をもとに,そこから考えられうる実際のゲームの完全な状況を列挙した集合のことを意味します. ↩
- \(\pi_{-i}^{\sigma^t}(I)\)は,戦略\(\sigma^t\)に従った場合に,プレイヤ \(i\)以外の要因によって\(I\)に到達する確率を表しています.つまり,プレイヤ \(i\)は必ず\(I\)へ向かうように振る舞うとした上での到達確率を表します. ↩
- \(\sum_{a\in A(I)} \max(R_i^T(I,a),0)<0\)の場合,単に\(\sigma_i^{T+1}(I,a)=\frac{1}{|A(I)|}\)とします. ↩
- CFRをさらに高速化したCFR+[3]というアルゴリズムでは\(10^{14}\)程度の情報集合数のゲームにおいても均衡戦略を計算できますが,それでも\(10^{16}\)は少し大きすぎます. ↩
- 実際には,見えているゲームの状況の他に,どういう行動履歴を辿ってその状況になったのか,ということもCFRプレイヤは考慮します. ↩
Author
