今回はちょっと変わった機械学習の評価方法を提案している論文の紹介です。
The Selective Labels Problem: Evaluating Algorithmic Predictions in the Presence of Unobservablesという論文で、2017年のKDDにて発表された物です。

人間の意思決定の結果を元のデータとして機械学習でより良い意思決定を行いたい場合に直面する問題を定義し、その中でより適正な評価方法を提案しているといった内容です。
AILabで行なっている論文読み会で発表した際の資料も参照してもらえればと。

意思決定ログの問題点

保釈の意思決定

この論文の中では裁判における保釈の意思決定をメインに取り扱っています。
判事は自分の担当する被告に対して保釈を許可するか否かを意思決定します（t = 1 or 0）。被告は保釈されると実社会に戻り、普通の生活をするか再び犯罪に手を染めるかを決定します(Y = 1 or 0)。保釈されなかった場合には収容所に収監されます(Y = NA)。
保釈を認めて期間中に再犯を起こされてしまうと社会的なコストが発生してしまうために、保釈した人が再犯するという状態はなるべく避けたいと判事は考えます。しかし誰彼構わず保釈を拒否するわけにも行きません。なぜなら収容所の運営コストは保釈されない被告の数が増えると増加してしまうからです。

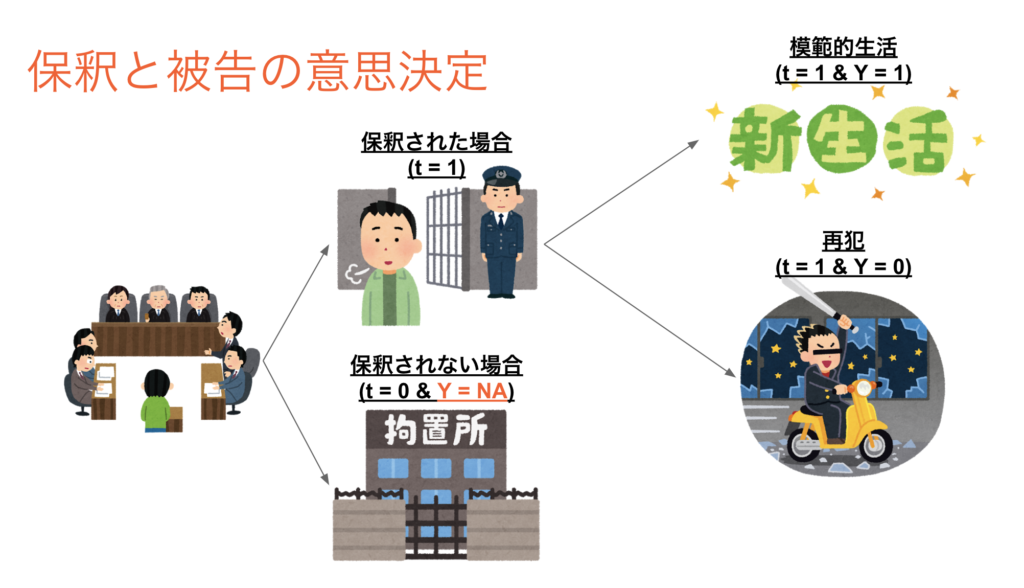
この事から、判事はなるべく再犯しそうな被告のみに対し保釈を拒否し、再犯しなさそうな場合には積極的に保釈を認めたいというインセンティブがある事になります。そして判事はそれぞれ自分が担当する被告について保釈した場合の再犯を起こす確率を予測し、それに基づいて意思決定を行います。このように意思決定のルールが整っている場合、予測問題を機械学習に入れ替えて保釈の意思決定を行う事は応用上良くある発想であるように思えます。

よくある二つの問題点

しかし、人間の意思決定データを入れ替えるような機械学習の応用は中々上手くいかないという事は多くの実務家の認識として存在するのではないでしょうか？

この論文ではその理由として２つの問題点に着目しています。

1. Unobserved
   これは人には利用できるが機械学習のモデルをつくるときには利用出来ない特徴量が存在しているという問題です。例えば判事は被告の法廷審問に参加する被告の家族の存在や被告自身の法廷審問時における態度などを観測してそれを元に再犯の確率を予測する事ができます。（家族が参加すると再犯しにくかったりする）しかし、これらの記録は公式には残らないので学習データには含まれません。

2. Selective Labels
   これは再犯するか否かというラベルが、判事が保釈を許可した場合に限って観測されるという問題です。判事は再犯しにくいと予測した被告を保釈するので、ラベルのついた学習データとしては再犯しにくい被告のデータばかりが集まるという事になります。

これらの問題はどちらか一方が存在する場合にはそれぞれ対処の方法が知られています。
Unobservedに関しては機械学習においては無視して学習をそのまま行なえば問題ありません。特徴量が不足する事により幾らか精度が下がってしまいますが、観測できなかった特徴量と相関の強い特徴量が学習データに含まれて入れば欠損した特徴の効果も幾らか含んで学習してくれます。
Selective Labeslの問題では因果推論のアイデアを応用する事で幾らか問題が解決できる事が知られています。例えば保釈されるか否かを分類問題で解き、その結果得られる予測確率でサンプルの重みをつけて再犯確率の予測を行うといった方法が考えられます。

組み合わせによる問題

しかし、これらの問題が同時に存在する場合には新たな問題が浮上します。
法廷審問に家族が参加するという特徴は、保釈後に被告が家族からの監視を受けて再犯しにくくなるという傾向があるために再犯率が下がる事が判事には知られています。そして被告の年齢が若い場合には家族が参加する確率が非常に高いという事も知られています。

この場合、多くの判事はこの特徴を踏まえて若くて家族が法廷審問に参加する被告を多く保釈します。一方で若いが家族が法廷審問に参加しなかった被告は中々保釈されません。このようなプロセスから学習データが生まれている場合、学習データでラベルが観測される若い被告の大半は家族が法廷審問に参加したものになり、ラベルが観測されない若い被告の大半は家族が法廷審問に参加しなかった者になります。

問題なのは機械学習のモデルにとっては家族の参加は観測できない特徴になっているという事です。これによりこの学習データで機械学習のモデルは若い被告は再犯率が低いといった相関関係を学習します。しかし実際にモデルをデプロイした際には家族が参加した場合もしなかった場合に対しても予測を行わなければならないため、被告が若い場合には誤差が大きくなってしまいます。

つまり、学習データでは「若い＝再犯率が低い」と学習する事が精度を改善する一方で、予測したいデータでは精度の改善には繋がらないという結果になってしまいます。この傾向が存在する場合、いくらCross-Validation等を利用して学習データの中で比較して精度が優っていたとしても実際の予測では性能が劣化して比較対象よりも精度が劣っているかもしれないという事がわかります。

提案されている評価方法

前提条件の確認

さて、この論文ではこのような状況の時に三つの条件を満たせればより良い評価ができるという事を説明しています。
* 複数の意思決定者（判事）から学習データが発生している事
* それぞれの意思決定者（判事）は案件（裁判）に対してランダムに選択されている事
* 意思決定者は結果を予測しながら意思決定を行い、意思決定の境界線がそれぞれ異なる事（同じ５０％の再犯率を予測した時に保釈を許可する判事もいれば許可しない判事もいる状態）

保釈の意思決定の例ではこのような条件を満たしています。しかし、社会の仕組みの中でこのような条件を満たすものはなかなか存在しない気がします。

ARとFRによる評価

評価自体も一般的に分類問題で用いられるAUCやloglossではなく、Failure Rate（FR）とAcceptance Rate（AR）というものを用います。ARとは保釈する割合の事をさします。例えばある判事が1000人の被告のうち７００人の被告に対して保釈を認める場合にはARは７０%となります。FRは被告の数に対して再犯が発生した割合の事をさします。例えばある判事が1000人のうち700人の被告に対して保釈を認め、そのうち100人が再犯を行なった場合FRは10%となります。

ARとFRを利用した評価はARを固定した状態で、FRを比較するという形で行われます。ARは保釈の数を示すので、収容所の社会的コストを表します。よって、ARを固定して保釈しないコストを同一にした状態で、FRをみる事でどれだけの再犯を許してしまったのかを比較する事が出来るわけです。

いくつかのARの値でFRをみる事で、AR-FR間の曲線を描く事が出来ます。モデル間や人の予測値でこのカーブを描き、比較する事でモデルの比較が可能になるというのがこの論文における基本的な評価方法です。この記事の中ではAR-FR間の曲線の事をAR-FRカーブと呼びます。

このカーブはイメージとしては以下のようなものになります。例えば黒のカーブが人の意思決定のカーブで、黒のカーブが機械学習モデルによるものであれば、同じARを見た時には機械学習モデルの方がFRが低いという事になり、機械学習を利用した意思決定がより良いという事がわかります。

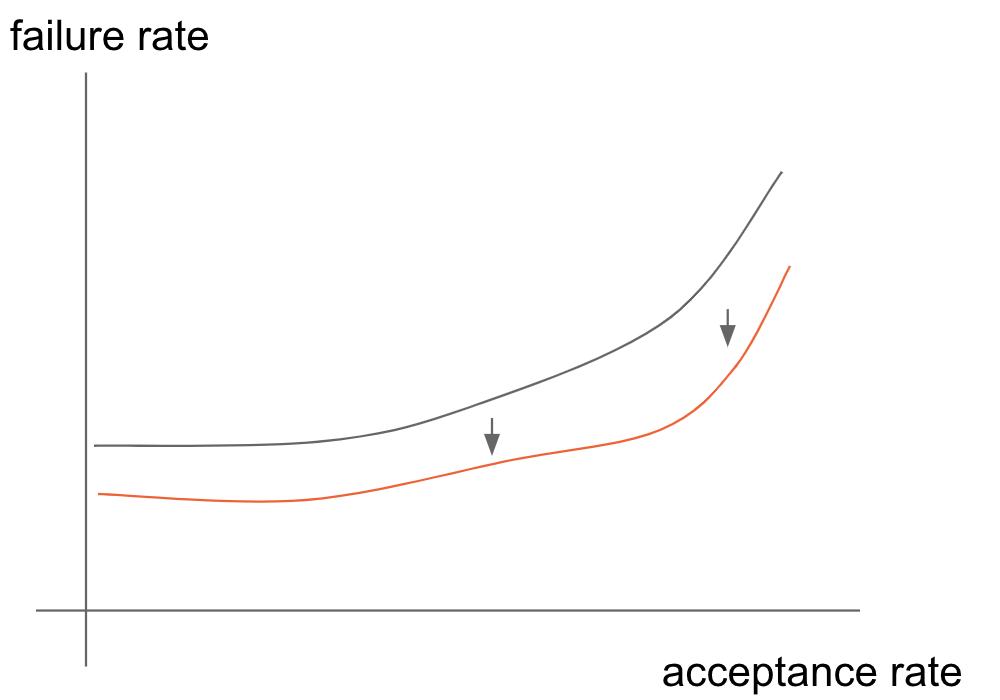
AR-FRカーブの描き方（Contraction Technique）

人の意思決定についてこのAR-FRカーブを描く事は非常に簡単です。想定している条件から、それぞれの判事が別々のARを持っているので、ARをそれぞれの判事のデータで集計してビン化してその中でFRを算出するだけでカーブを描く事ができます。

一方で機械学習のモデルでこのカーブを描く事は少し工夫が必要となります。この論文では別のデータで学習済みのモデル（B）がすでに手元にあるという状況を想定しています。

例えばAR = 60%の時のFRを算出したいとします。
1. まずは一番ARが高い意思決定者qのデータを持って来ます（\(AR_q\) = 90%）。サンプル数はNとします。
2. このデータに対してモデルBで再犯確率の予測値を算出します。
3. 実際にデータ上で保釈されていない被告のデータを捨てます。
4. さらに評価したいAR = 60%と同じになるまで予測された再犯確率の高いデータから捨てます。
5. 最後に残ったデータの中で再犯の数をカウントしてNで割ってFRを求めます。
これがあるAR = 60%を指定された時の機械学習のFRということになります。
これを各ARの値で算出する事でAR-FRのカーブを描く事ができます。
この方法をContraction Techniqueと命名しています。

少し怪しい部分

一番高いARを持つ意思決定者qのデータに対して予測値を出し、そのデータを絞るだけで何故FRの評価が出来てしまうのでしょうか？これはシンプルに意思決定者が各案件にランダムに選択されている為にデータの性質が同じである事が期待できるという点に基づいています。

このことから察しの良い方は「評価したいARをもつ意思決定者のデータと、ARが一番高い意思決定者のデータの質が実際には異なる場合には評価の質が下がるのでは？」という点が想定できると思います。これは例えばサンプル数が少ない場合などに想定されます。また、最初にARが高い意思決定者の決定をそのまま受け入れてデータを捨てる部分に関しては、モデルの純粋な評価では無くなってしまっているという点ではいささか不自然さを感じる部分かもしれません。

これらの点に関しては機械学習の予測値が実際の意思決定と食い違う場合にはFRの推定値の質が低下することが実験で示されています。（後述）

シミュレーションによる実験

実験の設計

では論文の中の実験内容について解説していきます。まずはシミュレーションデータでの実験です。
生成するデータは以下のような設定となっています。
裁判官の数:M = 100
裁判官一人当たりの裁判の数:500
裁判の数:N = 50,000
特徴量：X
裁判官のみに使える特徴量：Z
機械学習も裁判官も使えない特徴量：W
X,Z,Wはそれぞれ 平均０ 分散１の正規分布から生成
裁判官毎のAR：r
rは[0.1 – 0.9]の間で一様分布から生成してラウンドを取る

Y（再犯するか否か）の確率を計算する
$$P(Y = 0|X,Z,W) = \frac{1}{1 + \exp{-(\beta_X X + \beta_Z Z + \beta_W W)}}$$
確率が0.5以上であれば再犯したという設定にし、それ以外は再犯しないとする。
$$P(Y = 0|X,Z,W) > 0.5 \ then \ Y = 1\ else\ Y=0$$
このとき\(\beta_X = \beta_Z = 1\)で\(\beta_W = 0.2\)とする。

T（保釈するか否か）の作成は以下の様に行う
$$P(T = 0|X,Z,W) = \frac{1}{1 + \exp{-(\beta_X X + \beta_Z Z)}} + \epsilon$$
\(\epsilon\)は意思決定のノイズを表し、平均０分散０.１の正規分布から生成される。
各裁判官はそれぞれの持つr以下の\(P(T = 0|X,Z,W)\)を得た場合には保釈を拒否し（T = 0）、それ以外の場合には保釈を許可する（T = 1）。

この結果特徴X,Z,Wを持った裁判50000件に対して、ランダムに振られた裁判官・保釈されたか否か（T）・保釈すると再犯するか否か(Y)が全て観測されたデータが手に入ります。

モデルの学習

作成したデータセットをランダムに半分に分割し、片方を学習データとします。
学習データでは実際の状況を想定して保釈されたデータのみを残した状態で再犯の予測問題を学習します。実験の中ではロジスティック回帰が用いられています。

MLと人間のAR-FRカーブを描く

テストデータにおいて各裁判官毎にデータ上のARを算出して小数点１桁以下を切り、その値でグループ化してFRを集計します。これはARが似ている裁判官のデータを集めてあたかも一人の裁判からそれらのデータが生まれたかの様に扱う事と同じ操作です。これにより、人のAR-FRカーブを描くことができます。機械学習のカーブはこのグループ化されたデータに対して前述のプロセスを実行します。

結果人の意思決定と機械学習による意思決定のAR-FRカーブを描く事が出来ました。以下は実験の結果として得られたカーブとなっています。Human Evaluationが人間の意思決定で、Contractionが提案手法による機械学習の評価となっています。

比較対象のカーブを描く

この論文では比較対象としてTrue Evaluation, Labeled Outcome, Propensity Scoreの三つが存在します。
True EvaluationはモデルBによる予測値をテストデータの全てのサンプルに対して算出し、ARに応じて保釈の意思決定を上書きし、FRを計算するというものです。事前に振られている裁判官の保釈の意思決定を無視して機械学習による意思決定の評価をしているので、本番にこのモデルを投入した時にどんな評価を得られるかを示す値になっています。よって基本的にはこの評価とより近い評価を得られる方法が望ましいという事になります。
しかしこれは保釈されなかった被告に関しては本来再犯するかは観測できないため、シミュレーション実験上でのみ比較できる対象となります。

Labeled Outcomeはテストデータの裁判官によって保釈されている全てのデータに対してモデルBによる予測値を算出し、ARのグループ毎に下からAR%のサンプルで再犯が観測できたとしてFRを算出するといった方法です。元々1000人の被告に対して700人保釈するAR=70%のデータがある場合、その700人に対して再犯確率の予測値を算出して確率の低い490人を保釈したとしてその中で再犯数を集計します。結果70人が再犯していたとすると、70/700 = 10%がMLのFRという事になります。
これはもっともナイーブな評価方法ですが、実務的にはよく選択される方法な気がしています。

Propensity Scoreは保釈される確率をロジスティック回帰などで学習し、FRの算出の際に予測値の逆数をサンプルの重みとして使うといった事を行います。これは因果推論のアイデアを応用した場合の評価方法ですが、今回はunobservedの問題が存在するために上手く機能しない事が想定されています。

実験結果

AR-FRカーブの比較

以下が論文内で示されたシミュレーションデータにおける実験の結果です。
横軸がARで、縦軸がFRとなっています。

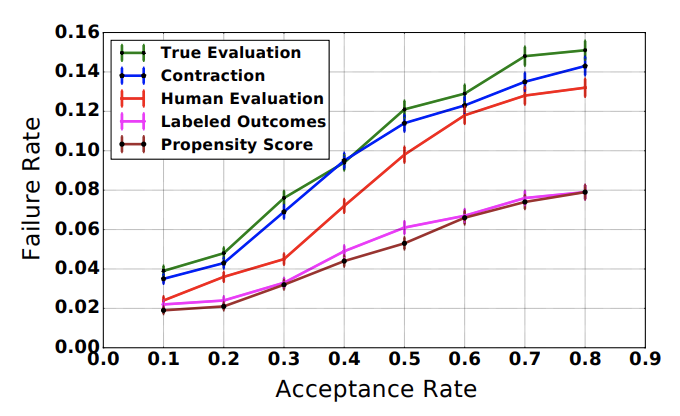
Human Evaluationは評価としての比較対象ではない事に注意してください。

実験の結果としてはTrue Evaluationに対してContractionがLabeled Outcome, Propensity Scoreよりも非常に近いという状態になっており、シミュレーション上はこの評価方法がベターである事を示しています。

また、比較している評価方法の場合、カーブがHuman Evaluationよりも下回るために人間の意思決定より機械学習を利用した意思決定の方が質が高いという結果をオフラインの検証で示す事になりますが、Contractionで評価を行なった場合にはその逆の結論を得る事になります。True EvaluationはHuman Evaluationよりも上側のカーブとなっているため、本番適応した際の機械学習の評価は人間の評価よりも低いという事になるため、Contractionによる評価がより適正であると言えるでしょう。

意思決定者しか使えない特徴の影響

家族の法廷審問への参加などの、意思決定者にのみ利用できる特徴量の影響がより大きくなった時に、それぞれの評価はどのように変化するのでしょうか？これを示しているのがこちらのグラフになります。

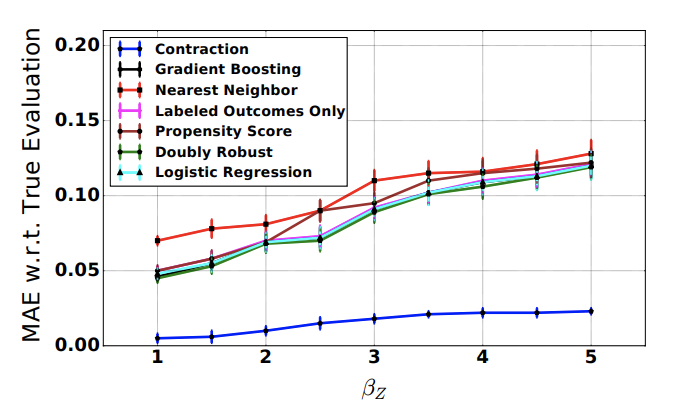
元々の値が１なので、右に行く毎に２倍、３倍となっていきます。縦軸はTrue Evaluationとの誤差をMAEで算出したものになっているので、下にあるほど誤差が少ない事を示しています。
比較対象は意思決定しゃにのみ利用できる特徴量の影響が大きくなる毎に誤差も大きくなっているのがわかります。先のグラフで比較対象が楽観的な方向性に誤差を持つ事がわかっているので、これはおそらく機械学習の意思決定が人間に圧倒的に勝るだろうという方向に誤差が大きくなっていると考えられます。一方でContractionは誤差が微増するものの、この変化に対しては頑健な性質を見せています。

ARが最も高い意思決定者（q）のデータの質による影響

ARが最も高い意思決定者のデータの質が悪い場合には推定結果の質も悪くなりそうだという話に対する実験結果が論文内では示されています。

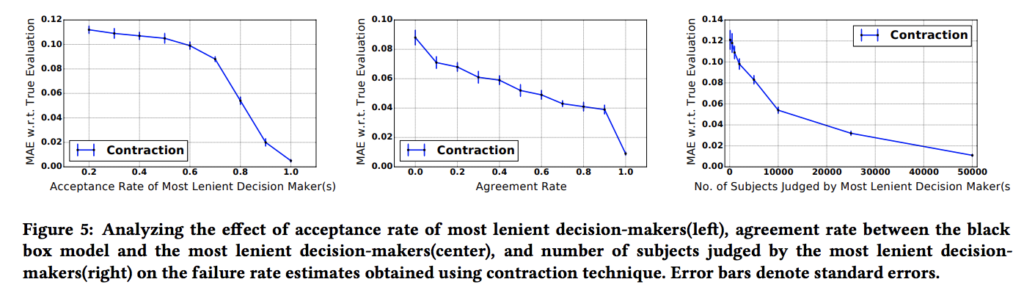
左の図は\(AR_q\)が横軸にとってあり、縦軸にContractionのTrue Evaluationに対する誤差をとったものになっています。これは\(AR_q\)が低くなっていった場合にContractionの誤差がどう変化するかを見るものとなっています。ここでは\(AR_q\)が下がると誤差が大きく上昇することが観測されています。

中央の図はARが最も高い意思決定者のデータで保釈されないような被告が機械学習のモデルで実際に保釈されないような意思決定になるか？という一致率（Agreement Rate）を横軸にとったものです。例えば裁判官qが1000人内100人に保釈を認めないとします。この時1000人に対して機械学習で再犯確率の予測値を算出し、その上位100人を見たときに、裁判官が保釈しなかった100人と一致した人数が30人の場合には一致率が30%という事になります。
この一致率も低下するとやはり評価の誤差が大きくなることが観測されています。

右の図は裁判官qのデータのサイズが誤差に与える影響を表しています。これはデータのサイズが大きくなるほど誤差が減少する事が観測されています。

この様に、AR-FRカーブによる評価の質は最もARが高い意思決定者の性質によって大きく左右されるということが示されています。

実データでの実験

この論文では三つの実データで評価を行なっています。

一つは今までと同様保釈の意思決定についてです。

もう一つは医師による処置の意思決定についてです。これは咳などの症状を訴える患者に対して、医師が服用期間が短くて効果の弱い処置を与えるか服用期間が長くて効果の強い処置を与えるかという選択を扱ったものです。15日以内に症状の再発が起きるか否かが予測したいラベルとなります。

三つ目は法人向けの保険の販売で、保険商品を作れるマネージャーが商品作成の依頼をもらった時にその商品を作るか否かという意思決定を扱います。商品を作った結果黒字になったか否かが予測したいラベルとなります。

この記事では細かく取り扱いませんが、意思決定者毎に与えられている案件の質が違うという可能性は統計的な検定で検証されています。それぞれの実験結果は以下のようになっています。

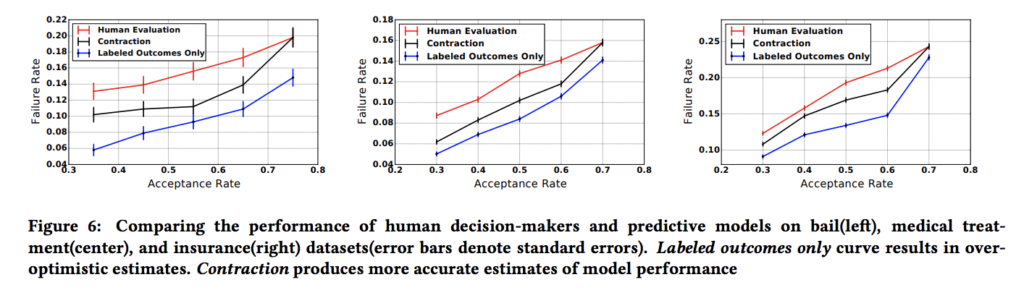
これらの実験の結果全てのケースにおいてContractionとLabeled Outcomeの結論が食い違う事がわかっています。つまり、手に入ったデータセットの背景を考慮せずにモデルの評価をナイーブに行うことは機械学習の評価を過剰に高める事になり、本番において大きなしっぺ返しをもらう事を示唆しています。

まとめと感想

内容としては「人の意思決定ログから機械学習を利用してよりベターな意思決定ルールを作る」という話に置いて重要になるオフライン評価法方法を提案したものでした。

意思決定者が案件に対してランダムにアサインされるなど、ビジネス上のケースでは中々達成されそうにない状況を仮定していたりするのですが、非常に面白い評価方法であるとともに根底で捉えている問題に関しては非常に本質的な問題を捉えているように思えました。