Blog
【採択論文紹介】Daycare Matching in Japan: Transfers and Siblings
AI Lab EconSIチームの孫と竹浪です。この記事では、人工知能分野のトップカンファレンスであるAAAI-23に採択されたSun et al. ”Daycare Matching in Japan: Transfers and Siblings” [1]について紹介します。本研究は孫を中心とし、竹浪、森脇、冨田および九州大学の横尾真教授により実施されました。論文のarxivバージョンはこちらです。
はじめに
保育所入所選考にはマッチング理論が応用できます。しかし、実務ではきょうだいや転園などに考慮する必要があるため、先行研究で提案されているアルゴリズムをそのまま実務に適用することはできません。そこで、本論文では実務で求められる性質を全て満たすアルゴリズムを整数計画法にてデザインしました。このアルゴリズムを実際のデータに適用したところ、実際の割り当てよりも少なくとも同等以上に望ましいマッチング結果を得ることができました。
保育所入所選考とマッチング理論
保育所を利用するときは、自治体で行う保育所入所選考を経る必要があります。
利用希望者は、居住している自治体に希望保育所名とその希望順位、世帯の就労状況等を記載した申請書を提出します。そして、自治体は申請された情報をもとに保育の必要性に応じた指数を決定し、指数順に児童を希望する保育所に割り当てます。まさに児童と保育所のマッチングです。AI Lab EconSIチームでは、マッチング理論による保育所入所選考の改善に取り組んでおり、東京大学マーケットデザインセンター(UTMD)と共同研究を行い、実際に東京都多摩市の制度変更に貢献しました。
保育所入所選考固有の問題
保育所入所選考を難しくさせる固有の問題として、きょうだいの存在と転園の存在があります。
きょうだい
異年齢・同年齢問わず、複数のきょうだいが同時に保育所を希望する場合があります。このとき応募者は、
- きょうだい全員を同時に入園させたいか、別の時期でも構わないか
- 同じ保育所への入園だけを希望するか、別々の保育所への入園でも構わないか
といった意思表示を行い、自治体に申請します。例えば、東京都渋谷区では希望の組み合わせを提出できるようになっています。自治体は、こうした希望に配慮して保育所を割り当てています。したがって、マッチングの際はきょうだいの希望の組み合わせを考慮する必要があります。
しかし、標準的なマッチングアルゴリズムではあくまで個人の割り当てを考えているため、きょうだいの希望の組み合わせを踏まえた割り当てには対応していません。例えば、きょうだい2名がともにA保育所が第一希望、B保育所を第二希望にしている場合、きょうだいが一緒に入れない(A保育所、B保育所)という組み合わせではなく、(B保育所、B保育所)の組み合わせを優先したいということがありえます。このように、きょうだいが希望する保育所の組み合わせのパターンによって希望順序が決まりますが、個人をもとにしたアルゴリズムではこうした構造を考慮できません。
転園
通園する保育所を変更したい場合、多くの自治体では転園を希望することができます。その際、転園希望者については、
- 希望する保育所に入園させる
- すでに入園している保育所(転園元)に戻る
のいずれかを実現し、待機児童にはさせない入所選考を行う必要があります。
さらに、
- 転園が成功すれば転園元に空きが出るため、希望者がいれば割り当てる必要がある
- きょうだいのうち1人が、あるいは全員が転園を希望する場合がある
ことにも留意する必要があります。
きょうだいと転園に関する先行研究
保育所入所選考におけるきょうだいと似た状況として、
- 学校選択制におけるきょうだいの申し込み
- 研修医マッチングにおけるカップルの存在
があります。

表1: 先行研究におけるきょうだいや転園の取り扱い状況([1]のTable 1を改変)
表1では、保育所入所選考においてきょうだいを取り扱うにあたり重要な学校選択制、研修医マッチング、保育所入所選考の先行研究における
- 転園
- きょうだい・カップル
- きょうだいの希望の組み合わせ
の取り扱い状況をまとめました。一番下の本論文を除き、
- 転園のことを検討していない[2,3,5,6,7]
- きょうだい(カップル)が2名の場合のみを検討しているため、2人より多いきょうだいがいる場合に対応していない[4,5,6]
- きょうだいの組み合わせに制約がある。例えばきょうだいが同じ学校のみを希望していると仮定しているが、実際にはきょうだいが別の保育所を希望する場合もある[7.8]
という状況であり、先行研究にて提案されているアルゴリズムをそのまま保育所入所選考に応用することができません。
実務において要求される性質
きょうだい、転園の他に、保育所入所選考の実務において要求される性質として、次のようなものがあります。
- 個人合理性:希望していない保育所に割り当てない
- 公平性:優先順位が高い人から順に割り当てる
- 非浪費性:「その保育所を希望する応募者がいるにもかかわらず受け入れ枠に空きがある状況」(浪費的な状況)をつくらない
したがって、保育所入所選考の実務においては、割り当ての結果が以下の制約を満たしている必要があります。
- きょうだいへの対応
- 転園への対応
- 個人合理性
- 公平性
- 非浪費性
本論文の貢献
そこで、本論文では上記した制約を満たす新たなアルゴリズムをデザインしました。本論文による貢献は次の通りです。
- 実際のデータに基づき、日本で実施されている保育所入所選考を現実的なモデルとして定式化しました。転園、きょうだい、制約のないきょうだいの希望の組み合わせを全て取り扱った研究は我々の知る限り初めてです。
- これまでのマッチング理論で用いられてきた個人合理性(Individual Rationality)、非浪費性(Non-wastefulness)、公平性に関連するブロッキングペア(Blocking Pair)といった概念を、転園やきょうだいの組み合わせを考慮することで一般化しました。具体的には、個人をベースに構成されていたこれらの概念を、家族をベースにし、それぞれ家族合理性(Family Rationality)、家族非浪費性(Family Non-wastefulness)、ブロッキング連合(Blocking Coalition)として定義しました。
- きょうだい、転園、家族合理性、公平性(ブロッキング連合がない状態)、家族非浪費性に対応したアルゴリズムを開発し、実装しました。
- 自治体から提供された匿名データにてアルゴリズムの性能を確認したところ、実際の割り当てと少なくとも同等、自治体によっては上回る結果を得られることを確認しました。
- きょうだい、転園、家族合理性、公平性、家族非浪費性といったすべての制約を満たす解が存在しない場合があり、実際に児童が4人(うち2人はきょうだい)の例でそのような場合を例示しています。しかし、シミュレーションで用いたすべての自治体のデータで、これらすべての制約を満たす解が求められました。
モデル
本論文ではきょうだいに対応するため、家族をベースにしたモデルを設定しています。本論文のモデルは、次のインスタンス\(I\)にて記述しています。
$$I = (C, F, D, G, \omega, \succ_{C}, \succ_{F}, \succ_{D}, q)$$
それぞれ次を意味します。
- \(C\):児童の集合
- \(F\):家族の集合
- \(D\):保育所の集合
- \(\omega(c)\):児童\(c\)の転園元(転園元がない場合にも対応)
- \(\succ_C\):\(D\)に対する各個人\(c \in C\)の選好順序\(\succ_c\)の集合
- \(\succ_F\):\(D\)に対する各家族\(f \in F\)に属する児童\(C_f\)の選好の組み合わせ\(\succ_f\)の集合
- \(\succ_D\):各個人\(c \in C\)に対する各保育所\(d \in D\)の優先順序\(\succ_d\)の集合
- \(q\):各保育所の募集人数のベクトル
各児童\(c\)はひとつの家族\(f \in F\)に所属し、各家族\(f\)は児童の集合\(C_f \subseteq C\)により構成されます。
アルゴリズム
アルゴリズムは線形計画法の整数バージョンである整数計画法によりモデリングされています。具体的には、きょうだいの希望の組み合わせ、転園を考慮しつつ、家族合理性、公平性(ブロッキング連合がない状態)、家族非浪費性の制約下で、マッチングされる児童を最大化(待機児童を最小化)する問題を整数計画法により解いています。興味のある方は論文をご覧ください。
自治体データを用いたシミュレーション
実際の割り当ての結果と今回デザインしたアルゴリズムの結果の違いについて解説します。東京都の渋谷区と多摩市から提供された2021 年度と 2022 年度の一斉入所における希望者データ(匿名加工処理済み)と保育所データに対して、このアルゴリズムを用いたシミュレーションを行いました。そこで、各自治体における実際の割り当て結果とシミュレーションの結果とを比較・考察します。
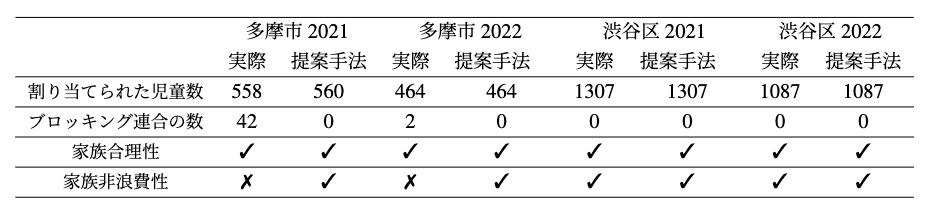
表2: 実際の割り当て結果と本論文で提案されたアルゴリズムの割り当て結果の比較([1]のTable 2を改変)
表2は、各自治体における実際の割り当て結果と本論文で提案されたアルゴリズム(提案手法)の割り当て結果を比較したものです。この表から 2 つのことが言えます。
- 各自治体で性質の良い割り当てや待機児童が少ない割り当てが達成できました。多摩市においては、今回実装したアルゴリズム(提案手法)を用いることで実際の結果と同等以上に児童を割り当てているだけではなく、家族合理性と家族非浪費性を満たしています。また、渋谷区においては、実際のマッチングと同一の結果が得られました。
- いずれの自治体、年度においてもアルゴリズム(提案手法)により公平性(ブロッキング連合がない状態)を満たすマッチング結果を得ることができました。
アルゴリズムの社会実装
AI LabとGovTech開発センターは、この論文で示されたアルゴリズムを用いた自治体向け保育所入所選考システムを開発しています。研究に基づいた保育所入所選考システムにご興味のある自治体の方はこちらからご連絡をください。
参考文献
[1] Sun, Z., Y. Takenami, D. Moriwaki, Y. Tomita, and M. Yokoo (in press) ”Daycare Matching in Japan: Transfers and Siblings”, AAAI, Thirty-Seventh AAAI Conference on Artificial Intelligence
[2] Biró, P.; Manlove, D. F.; and McBride, I. 2014. The hospitals/residents problem with couples: Complexity and integer programming models. In International Symposium on Experimental Algorithms, 10–21. Springer.
[3]Manlove, D. F.; McBride, I.; and Trimble, J. 2017. “Almost stable” matchings in the Hospitals/Residents problem with
Couples. Constraints, 22(1): 50–72.
[4]Hamada, N.; Hsu, C.; Kurata, R.; Suzuki, T.; Ueda, S.; and Yokoo, M. 2017. Strategy-proof school choice mechanisms with minimum quotas and initial endowments. Artificial Intelligence, 249: 47–71.
[5]Okumura, Y. 2019. School choice with general constraints: a market design approach for the nursery school waiting list problem in Japan. The Japanese Economic Review, 70(4): 497–516.
[6]Kamada, Y.; and Kojima, F. 2020. Fair matching under constraints: Theory and applications. Review of Economic Studies.
[7]Dur, U.; Morrill, T.; and Phan, W. 2022. Family Ties: School Assignment with Siblings. Theoretical Economics, 17(1): 89–120.
[8]Correa, J.; Epstein, N.; Epstein, R.; Escobar, J.; Rios, I.; Aramayo, N.; Bahamondes, B.; Bonet, C.; Castillo, M.; Cristi, A.; Epstein, B.; and Subiabre, F. 2022. School choice in Chile. Operations Research, 70(2): 1066–1087.
Author
