AI Lab EconSIチームの孫です。この記事では、外部性のもとで公平分割問題に関する研究について紹介します。この研究成果はニューサウスウェールズ大学のHaris Aziz准教授(Scientia Associate Professor)とToby Walsh教授(Laureate Fellow & Scientia Professor)及びシンガポール国立大学のWarut Suksompong助教授(NUS Presidential Young Professor)との共同研究成果であり、人工知能分野において有名な国際会議であるAAAI 2023に採択されています。論文のリンクはこちらです。

公平分割問題

公平分割問題とは、参加者全員が各自の基準で公平と感じる方法で、有限な資源を配分できるかという問題です。領土や石油などの貴重な資源の配分に限らず、家賃や家事の分担、遺産の相続、離婚する際の財産分与などの日常生活への応用も多いです。

問題設定

財の集合を \( A=\{a_1, \cdots, a_m\} \)、参加者の集合を\(N=\{1, \cdots, n\}\)、全ての財の分割を\(\pi = \{\pi_1,\cdots, \pi_n\}\)とする。ここで、\(\bigcup_{i=1}^n \pi_i = A\)で、参加者 \(i\neq j\) のとき、\(\pi_i \cap \pi_j = \emptyset\)です。多くの既存文献では、各参加者が自分に割り当てられる財のみを評価します。一方で本研究では、他人に割り当てられる財も考慮して評価を行う設定である、「外部性」のもとでの公平分割問題について考察しました。\(V_i(j, a)\)を財 \(a\) が参加者 \(j\) に割り当てられる時の参加者 \(i\) の評価とします。参加者\(i\)の分割\(\pi\)の評価を\(V_i(\pi)\)は、各財の割り当てに対しての評価の和によって以下のように与えられます：\(V_i(\pi) = \sum_{a\in A} V_i(\pi(a), a)\)。ここで、 \(\pi(a)\) は分割 \(\pi\) において財 \(a\) を割り当てられる参加者を指します。

既存の公平性の概念

公平分割問題において、よく使われている概念は無羨望性 (envy-free)と比例性 (proportionality)です。無羨望であるとは各参加者が他人の財の割り当てを羨むことがない状態を意味し、比例公平性とは各参加者が全ての財の1/n（参加者の数）以上をもらう状態を意味します。非分割財の場合は，無羨望性を満たす財の割り当てが必ずしも存在しないため、近年、無羨望性を緩和した以下の概念が盛んに研究されています。

EF1（Envy-freeness up to 1 good）とは、全ての参加者\(i, j \in N\)に対して、「\(j\)の割り当てからある一つの財を削除することで、 あるいは、\(i\) の割り当てからある一つの負担を削除することで、\(i\) が\(j\)を羨むことがないようにできる状態」を指します．

EFx（Envy-freeness up to any good）とは、全ての参加者\(i, j \in N\)に対して、「 \(j\)の割り当てから任意の財を削除することで、あるいは、\(i\)の割り当てから任意の負担を削除することで、\(i\)が\(j\)を羨むことがないようにできる状態」を指します．

Velez [8]は外部性のもとでの無羨望性を以下のように修正しています。全ての参加者\(i, j \in N\)に対して、以下のような\(i, j\)が存在しないこと：

$$V_i(\pi^{i \leftrightarrow j}) > V_i(\pi)$$

ここで、\(\pi^{i \leftrightarrow j}\)は参加者 \(i\) と \(j[\)] が各自の割り当てを交換したときの分割とします。

概要

本研究では、従来のEF1とEFxの定義を外部性のもとでの非分割財の公平分割問題へと拡張し、新しい公平性の概念を提案しました。つづいて，参加者が二人の場合、EF1とEFxを満たす割り当てが常に存在する一方で，参加者が三人の場合、EFxを満たす割り当てが必ずしも存在しないことを証明しました。また，三人の参加者の選好に特定の仮定をおいた場合、EF1を満たす割り当てが必ず存在することも証明しました。さらに、比例公平性に基づくgeneral fair share (GFS)とgeneral fair share up to 1 item (GFS-1)という定義を提案し、参加者の人数に関わらずGFS-1を満たす割り当てが必ず存在することも証明しました。最後に，既存の公平性と本研究で提案した公平性の概念が以下のような関係性を持つことを示しました．

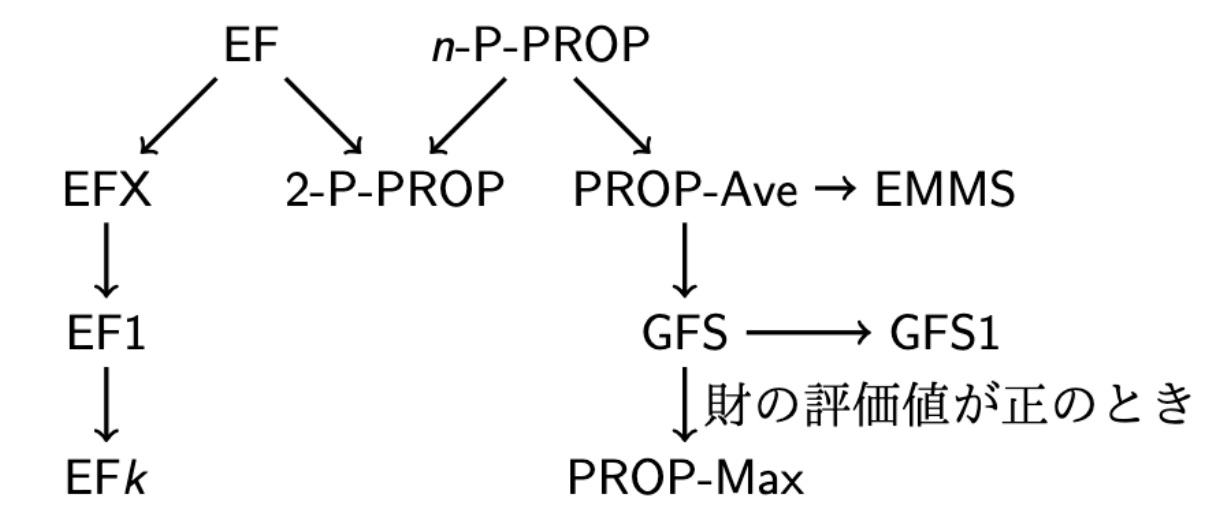まとめ

この研究では，外部性を考慮した公平性の概念を提案し、その性質と関係性について分析しました。また、各公平性の概念のもとで，「公平な割り当てが必ず存在するか」ということや，「どうやって公平な割り当てを計算するか」という二つの問題について検討しました。ご興味のある方はぜひ論文を読んでいただきたいと思います。

参考文献

[1] Amanatidis, G.; Birmpas, G.; Filos-Ratsikas, A.; and Voudouris, A. A. 2022. Fair division of indivisible goods: a survey. In Proceedings of the 31st International Joint Conference on Artificial Intelligence (IJCAI), 5385–5393.

[2] Aziz, H.; Bouveret, S.; Caragiannis, I.; Giagkousi, I.; and Lang, J. 2018. Knowledge, fairness, and social constraints. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence (AAAI), 4638–4645

[3] Aziz, H.; Caragiannis, I.; Igarashi, A.; and Walsh, T. 2022a. Fair allocation of indivisible goods and chores. Autonomous Agents and Multi-Agent Systems (JAAMAS), 36(1): 3:1–3:21

[4] Caragiannis, I.; Kurokawa, D.; Moulin, H.; Procaccia, A. D.; Shah, N.; and Wang, J. 2019. The unreasonable fairness of maximum Nash welfare. ACM Transactions on Economics and Computation (ACM-EC), 7(3): 12:1–12:32

[5] Conitzer, V.; Freeman, R.; and Shah, N. 2017. Fair public decision making. In Proceedings of the 18th ACM Conference on Economics and Computation (ACM-EC), 629–646

[6] Lipton, R. J.; Markakis, E.; Mossel, E.; and Saberi, A. 2004. On approximately fair allocations of indivisible goods. In Proceedings of the 5th ACM Conference on Economics and Computation (ACM-EC), 125–131

[7] Seddighin, M.; Saleh, H.; and Ghodsi, M. 2021. Maximin share guarantee for goods with positive externalities. Social Choice and Welfare, 56(2): 291–324

[8] Velez, R. A. 2016. Fairness and externalities. Theoretical Economics, 11(1): 381–410