AI Lab Algorithmsチームの濱野です．本稿では，連続変数とカテゴリ変数を両方含むブラックボックス最適化問題に適用可能な手法を提案した研究について解説します．本研究成果は，進化計算分野におけるトップカンファレンスであるGECCO2024に採択されています．

Ryoki Hamano, Shota Saito, Masahiro Nomura, Kento Uchida, and Shinichi Shirakawa. CatCMA : Stochastic Optimization for Mixed-Category Problems. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ’24), 2024. [arXiv] [GitHub]

本研究が対象とする問題

最適化問題とは，ある目的関数を最小化あるいは最大化するような変数を発見する問題のことを指します．目的関数が明示的に与えられている場合は，目的関数の微分情報などを用いて最適化を行うことができます．一方で，産業や科学の領域では目的関数が明示的に与えられないケースが存在し，そのような最適化問題はブラックボックス最適化問題と呼ばれています．ブラックボックス最適化問題では，入力となる変数とそれに対応する目的関数値の関係のみを用いて最適化を行うことになります．

本研究では，連続変数とカテゴリ変数を両方含むブラックボックス最適化問題（混合カテゴリブラックボックス最適化問題）を対象としています．カテゴリ変数は離散変数の一種で，複数の選択肢から一つを選ぶような変数のことを指します．例えば機械学習モデルのハイパーパラメータ最適化問題では，連続変数として“学習率”，カテゴリ変数として“オプティマイザの選択”などが最適化対象となります．ブラックボックス最適化の手法は，連続変数のみ，あるいは離散変数のみを対象をしたものがほとんどで，混合カテゴリブラックボックス最適化問題を対象とする手法は非常に限られていたという背景がありました．

提案手法：CatCMA

本研究では，多変量ガウス分布とカテゴリ分布の同時分布を用いた確率的最適化法であるCatCMAを提案しました．CatCMAにおける分布パラメータの更新式はInformation Geometric Optimization (IGO) [1]という確率的自然勾配法のフレームワークにもとづいて導出されています．IGOに関する詳細な説明はこちらの記事をご参照ください．またCatCMAでは，ブラックボックス連続最適化の有力な手法であるCMA-ES [2]の更新方法などが加えて導入されており，より強力な最適化性能を発揮することができます．

本稿では，CatCMAにおいて同時分布を安定的かつ効率的に更新する工夫点について紹介していきます．

カテゴリ分布更新時の問題

カテゴリ分布は各カテゴリの生成確率を分布パラメータとしてもっていますが，分布が探索初期に収束してしまうと，対応するカテゴリがほとんど生成されなくなってしまう問題が発生します．そこで，カテゴリ分布の更新時にマージン補正と呼ばれる操作を行うことでこの問題に対処します．マージン補正では，全ての分布パラメータが事前に決められた一定値（マージン）以上になるように調整を行います．そうすることで，どのカテゴリについても分布から一定以上の確率で生成されることが保証されます．

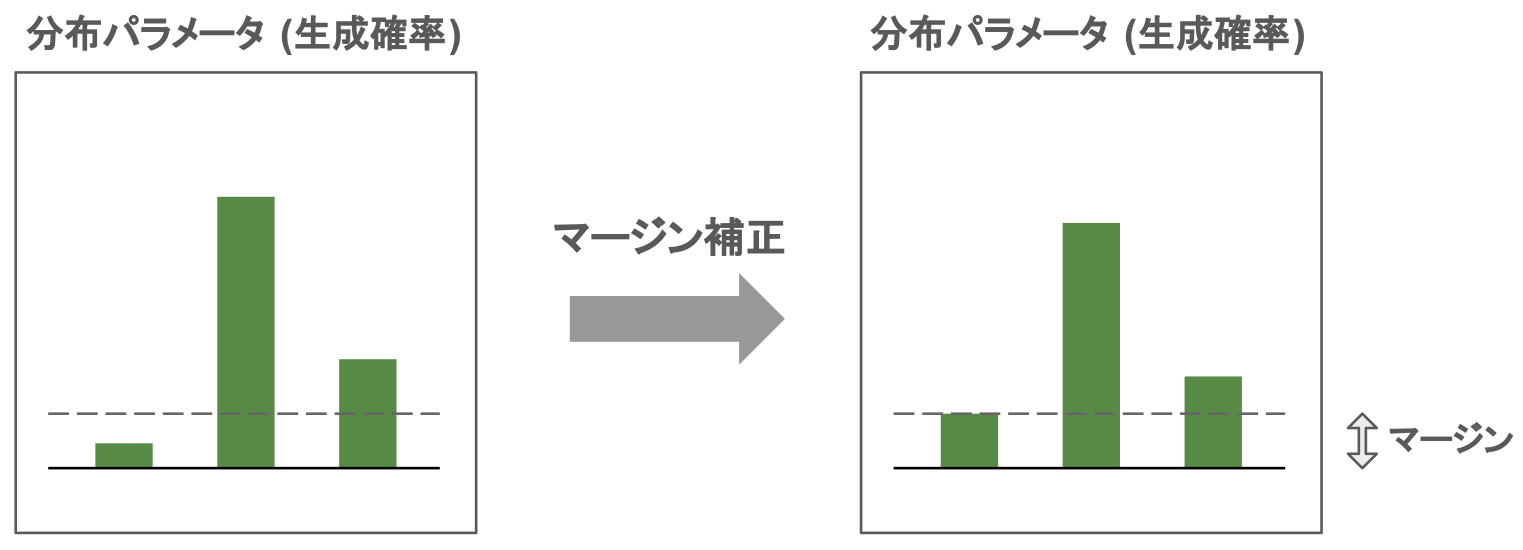
図1. マージン補正前後のカテゴリ分布の分布パラメータ．

しかし，今回のように多変量ガウス分布とカテゴリ分布の同時分布を更新する場合，マージンの値は小さすぎても大きすぎても最適化がうまくいかないことが本研究で明らかになっています．

そこで本研究では「最適化に悪影響を与える解の生成確率が十分小さくなるマージンの範囲」を解析的に導出し，その範囲内で最大となるマージンを推奨値として設定することで上記の問題を解決しました．実際に推奨値を使用した場合，様々な問題設定において安定的かつ効率的に最適化が行えていることを確認しています．

比較実験

実問題の最適化で重要となる性質をもつベンチマーク関数を用いて，混合カテゴリブラックボックス最適化のstate-of-the-artな手法であるCASMOPOLITAN [3]と，ハイパーパラメータ最適化でよく用いられるTPE [4]との比較実験を行いました．ある程度評価回数の予算がある場合，CatCMAは両手法を上回る性能を達成しています．さらに，CatCMAにおける優位性は目的関数の変数が多い場合により顕著になることを確認しています．

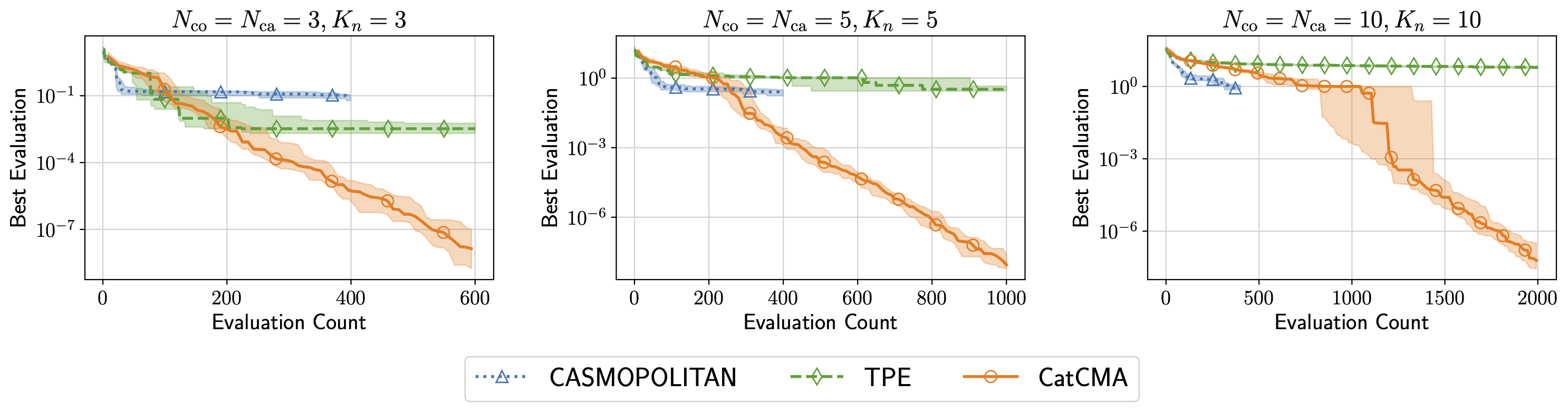
図2. 最適化中の解の最良評価値の推移．横軸は目的関数の評価回数，縦軸は最良評価値で小さいほど良い．連続変数の次元数，カテゴリ変数の次元数，カテゴリの種類数が 3 (左), 5 (中), 10 (右) の場合の結果．CASMOPOLITANはアルゴリズム内部の計算時間の都合上，評価回数に制限を設けている．

さいごに

本研究では混合カテゴリブラックボックス最適化に対する有力な手法としてCatCMAを提案しました．CatCMAは，連続変数と整数変数の同時最適化手法であるCMA-ES with Marginと組み合わせることが原理的に可能で，今後は連続変数，整数変数，カテゴリ変数の同時最適化が可能となることが期待されています．CatCMAについて気になった方は，ぜひ論文を読んだり，Python実装を使ってみたりしていただければ幸いです．

参考文献

[1] Yann Ollivier, Ludovic Arnold, Anne Auger, and Nikolaus Hansen. Information-geometric optimization algorithms: A unifying picture via invariance principles. The Journal of Machine Learning Research, 18(1):564–628, 2017.

[2] Nikolaus Hansen. The CMA Evolution Strategy: A tutorial. arXiv preprint arXiv:1604.00772, 2016.

[3] Xingchen Wan, Vu Nguyen, Huong Ha, Binxin Ru, Cong Lu, and Michael A. Osborne. Think Global and Act Local: Bayesian Optimisation over High-Dimensional Categorical and Mixed Search Spaces. In Proceedings of the 38th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 139), 2021.

[4] James Bergstra, Rémi Bardenet, Yoshua Bengio, and Balázs Kégl. Algorithms for Hyper-Parameter Optimization. In Advances in Neural Information Processing Systems, Vol. 24, 2011.