Blog
【採択論文紹介】Natural Gradient Interpretation of Rank-One Update in CMA-ES (PPSN2024)
AI Lab Algorithmsチームの濱野です.本稿では,有望なブラックボックス最適化法であるCMA-ESの更新方法に対して自然勾配の枠組みから新たな解釈を与えた研究について解説します.本研究成果は,進化計算分野におけるトップカンファレンスであるPPSN2024に採択されています.
Ryoki Hamano, Shinichi Shirakawa, and Masahiro Nomura. Natural Gradient Interpretation of Rank-One Update in CMA-ES. In Proceedings of the 18th International Conference on Parallel Problem Solving from Nature (PPSN’24), 2024. [arXiv]
背景:CMA-ESと理論的解釈
Covariance Matrix Adaptation Evolution Strategy (CMA-ES) [1, 2]は,ブラックボックス連続最適化を行う有望な進化計算法の一つです.CMA-ESは1996年にHansenら [1]によって提案され,産業から機械学習まで,様々な分野に応用されてきました.CMA-ESは多変量ガウス分布を用いた確率的な探索手法で,分布からの解の生成,解の評価,評価情報にもとづく分布の更新を繰り返すことで探索を行います.
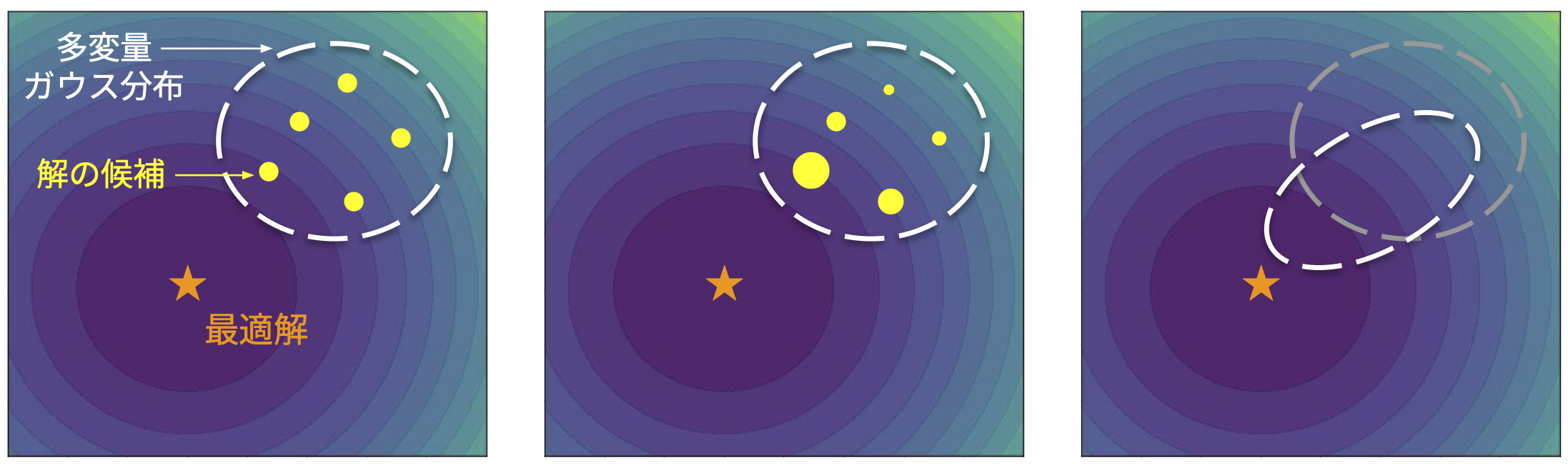
図1. CMA-ESのアルゴリズムの流れ.多変量ガウス分布から生成された解の候補を目的関数で評価して重みづけし,より良い解がより生成されやすくなるように分布を更新する.
近年では,CMA-ESをはじめとした進化計算法を理論的な観点から再解釈するための研究が行われています.その中でも,様々な進化計算法を情報幾何の観点から一般化したフレームワークであるInformation Geometric Optimization (IGO) [3]が注目されています.IGOによってアルゴリズムに理論保証を与えたり,新たなアルゴリズムへ拡張したりすることが可能となります.IGOの詳細についてはこちらの記事をご参照ください.
IGOフレームワークで扱う確率分布に多変量ガウス分布を適用することで,CMA-ES更新式の“一部”を復元することが可能であり,復元される更新式は確率的な自然勾配法として解釈することができていました.しかし,CMA-ESにおけるrank-one updateと呼ばれる更新式はIGOのような自然勾配の枠組みでは説明することができませんでした.
CMA-ESでは,過去の更新情報を進化パスと呼ばれるベクトルに累積していて,rank-one updateではこの進化パスを利用した更新を行います.具体的に,進化パスは多変量ガウス分布の平均ベクトルの更新差分を累積していて,rank-one updateは進化パスの方向に引きのばすように多変量ガウス分布を更新します.そうすることで,平均ベクトルの移動方向に解の候補が生成されやすくなり,分布の更新が効率化されることを期待します.
本研究のアプローチ
本研究では,rank-one updateに対して自然勾配の枠組みから解釈を与えることを目的とします.具体的には,以下の手順でrank-one updateの更新式を復元することを考えます.
- IGOをMAP推定の枠組みで拡張したMAP-IGOを新たに導出し,IGOで扱う確率分布パラメータに対して事前分布を設定できるようにする
- MAP-IGOの確率分布に多変量ガウス分布を,事前分布にNormal-inverse-Wishart分布を適用する
- 事前分布の分布パラメータを,rank-one updateのコンセプトにもとづいて設定することでrank-one updateの更新式を復元する
それぞれのステップについて簡潔に説明していきます.
1. MAP-IGOの提案
CMA-ESが「連続変数の空間に対して多変量ガウス分布を定義し,最適化を行う手法」であったのに対し,IGOは「任意の変数空間に対して対応する確率分布を定義し,アルゴリズムを導出するフレームワーク」であると言えます.IGOは最適化中のある時刻の情報(その時刻の確率分布,その時刻に生成された解)だけにもとづいて確率分布を更新するため,過去の更新情報を利用するrank-one updateは原理的にIGOから導出することができません.
そこで本研究では,この「過去の更新情報」を追加的に考慮できるようIGOを拡張したMAP-IGOを提案しています.MAP-IGOではMAP推定(Maximum a Posteriori Estimation)と同様に,解を生成する確率分布のパラメータに対して事前分布を設定することができます.この事前分布を用いて「過去の更新情報」を反映させようというアイディアです.
2. 事前分布の設定
本研究の目的は,rank-one updateを含むCMA-ESの更新式を導出することです.そのためMAP-IGOにおいて,解を生成する確率分布に多変量ガウス分布を,事前分布にNormal-inverse-Wishart分布を適用することを考えます.Normal-inverse-Wishart分布は多変量ガウス分布の共役事前分布です.MAP-IGOにおいて更新式を導出するには,各確率分布の対数尤度の自然勾配を導出する必要がありますが,それらはclosedにもとまることが本論文中で示されています.
3. 事前分布のパラメータを設定し,rank-one updateを導出
結論から述べると「平均ベクトルの移動しつつある方向に望ましい平均ベクトルが存在している」というアイディアを,事前分布パラメータの設定を通じて導入することでrank-one updateを復元することができます.では,具体的な事前分布パラメータの設定方法について説明します.Normal-inverse-Wishart分布には,多変量ガウス分布の平均ベクトルに関するパラメータ \(\delta, \gamma\) と,分散共分散行列に関するパラメータ \(\Psi, \nu\) があります.とくに, \(\delta\) は「多変量ガウス分布の平均ベクトルの期待値」を表していて,「平均ベクトルがおおよそどの位置にあるか」といった情報を考慮することができます.
CMA-ESにおいて進化パスは平均ベクトルの更新差分を累積していることを最初に説明しました.「平均ベクトルの移動しつつある方向」が進化パス \(p^{(t+1)}\) によって得られているとすると,望ましい平均ベクトルの位置は,現在の平均ベクトル \(m^{(t)}\) から進化パスの方向に移動した \(m^{(t)} + r \sigma^{(t)} p^{(t+1)}\) であると考えることができます.ここで, \(r\) は正の定数, \(\sigma^{(t)}\) はステップサイズです.これを \(\delta\) に設定し,適宜スケールが合うようにその他のパラメータを設定することで次のような更新式を得ます.
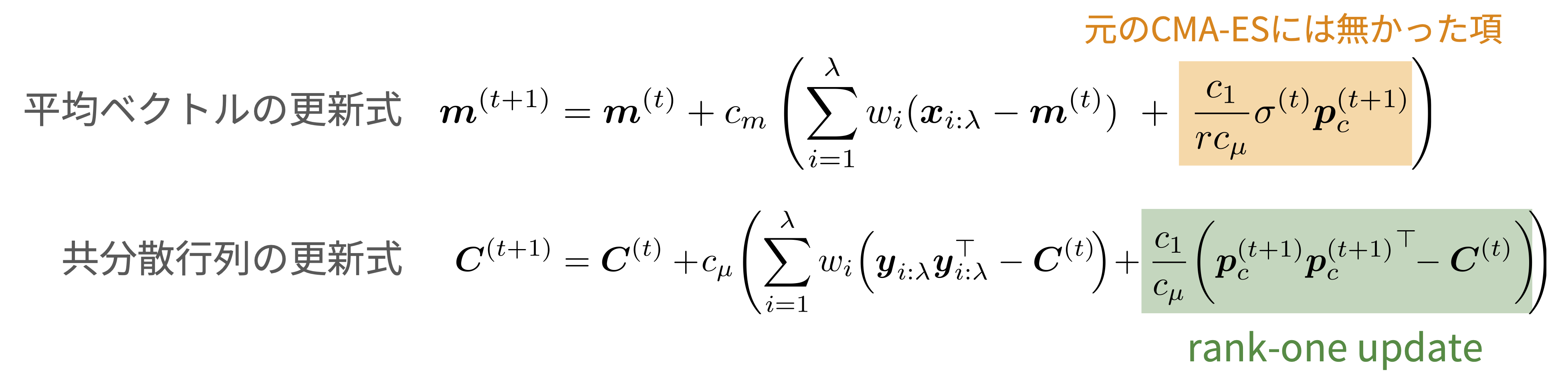
ここで,rank-one updateを復元することはできたものの,平均ベクトルの更新式に「元のCMA-ESにはなかった項」が現れています.ですが,この項は \(r\) の極限をとることで消去することが可能で,CMA-ESの更新式を復元することができます.この \(r\) の極限に対する解釈についても論文中で議論していますので,気になった方は論文をご参照ください.
新たに現れた項に対する解釈・実験的な調査
定数 \(r\) の極限をとることでCMA-ESの更新式をそのまま復元することができますが,試しに極限をとらずに有限の値を \(r\) に設定してみます.このとき新たに現れた項は消去されずに残りますが,この項は「平均ベクトルの更新差分を累積している進化パスを含んでいる」という点から勾配法におけるモメンタム項のような役割をすると考えることができます.本論文では,この項を追加したCMA-ESをMAP-CMAとして提案しており,MAP-CMAがどのような挙動をするか実験的に調査しています.
図2は,ベンチマーク関数であるRosenbrock関数をCMA-ESとMAP-CMAでそれぞれ最適化した際の平均ベクトルの推移を表しています.MAP-CMAは新たに追加された項によって,CMA-ESよりも平均ベクトルの移動を効率的に行えていることがわかります.
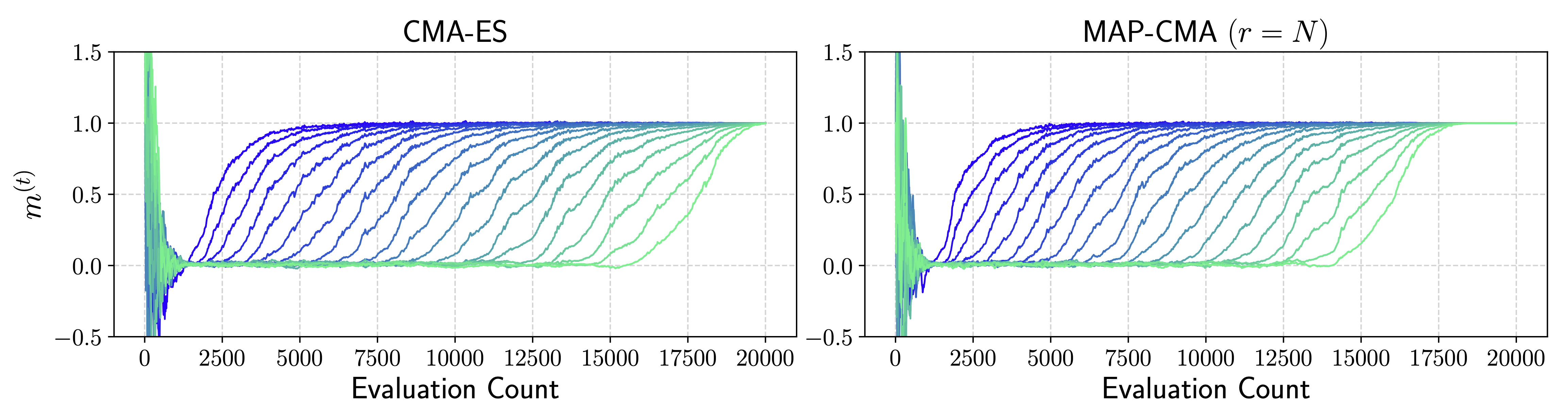
図2. 20次元のRosenbrock関数をCMA-ESとMAP-CMAでそれぞれ最適化した典型的な1試行の結果.MAP-CMAでは \(r\) は目的関数の次元数で設定した.最適化中の平均ベクトルについて各次元の推移を表示している.Rosenbrock関数の場合,最適解は \((1, \ldots, 1)\) となっており,最終的に平均ベクトルも \((1, \ldots, 1)\) 付近に移動している.
しかし別のベンチマーク関数では,MAP-CMAよりもCMA-ESの方が優れているケースや,両者で差がつかないケースもあり,一概にMAP-CMAの方が優れているとは言えないという結果になりました.(別のベンチマーク関数による結果や定数 \(r\) を別の値に設定した場合の結果については論文をご参照ください)
さいごに
本研究ではCMA-ESにおけるrank-one updateに対して,自然勾配の枠組みから新たな解釈を与えました.また,rank-one updateを復元する過程で新たに現れた項について実験的に調査を行いました.各導出について気になった方は,ぜひ論文を読んでいただければ幸いです.
参考文献
[1] Nikolaus Hansen and Andreas Ostermeier. Adapting arbitrary normal mutation distributions in evolution strategies: The covariance matrix adaptation. Proceedings of the IEEE Conference on Evolutionary Computation. 312 – 317, 1996.
[2] Nikolaus Hansen. The CMA Evolution Strategy: A tutorial. arXiv preprint arXiv:1604.00772, 2016.
[3] Yann Ollivier, Ludovic Arnold, Anne Auger, and Nikolaus Hansen. Information-geometric optimization algorithms: A unifying picture via invariance principles. The Journal of Machine Learning Research, 18(1):564–628, 2017.
Author
